
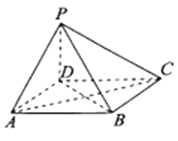
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為平行四邊形,
為平行四邊形,![]() 平面
平面![]() ,
,![]() .
.
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() 與平面
與平面![]() 所成角為45°,求二面角
所成角為45°,求二面角![]() 的大小.
的大小.
科目:高中數學 來源: 題型:
【題目】某公司有![]() 四輛汽車,其中
四輛汽車,其中![]() 車的車牌尾號為0,
車的車牌尾號為0,![]() 兩輛車的車牌尾號為6,
兩輛車的車牌尾號為6,![]() 車的車牌尾號為5,已知在非限行日,每輛車都有可能出車或不出車.已知
車的車牌尾號為5,已知在非限行日,每輛車都有可能出車或不出車.已知![]() 兩輛汽車每天出車的概率為
兩輛汽車每天出車的概率為![]() ,
,![]() 兩輛汽車每天出車的概率為
兩輛汽車每天出車的概率為![]() ,且四輛汽車是否出車是相互獨立的.
,且四輛汽車是否出車是相互獨立的.
該公司所在地區汽車限行規定如下:

(1)求該公司在星期四至少有2輛汽車出車的概率;
(2)設![]() 表示該公司在星期一和星期二兩天出車的車輛數之和,求
表示該公司在星期一和星期二兩天出車的車輛數之和,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著社會發展對環保的要求,越來越多的燃油汽車被電動汽車取代,為了了解某品牌的電動汽車的節能情況,對某一輛電動汽車“行車數據”的兩次記錄如下表:
記錄時間 | 累計里程 (單位:公里) | 平均耗電量(單位: | 剩余續航里程 (單位:公里) |
2020年1月1日 | 5000 | 0.125 | 380 |
2020年1月2日 | 5100 | 0.126 | 246 |
(注:累計里程指汽車從出廠開始累計行駛的路程,累計耗電量指汽車從出廠開始累計消耗的電量,![]()
![]() )
)
下面對該車在兩次記錄時間段內行駛100公里的耗電量估計正確的是( )
A.等于![]() B.
B.![]() 到
到![]() 之間C.等于
之間C.等于![]() D.大于
D.大于![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在△ABC中,角A,B,C所對的邊分別為a,b,c,其中A為銳角,且asin(B+C)是![]() bcosC與
bcosC與![]() ccosB的等差中項.
ccosB的等差中項.
(1)求角A的大小;
(2)若點D在△ABC的內部,且滿足∠CAD=∠ABD![]() ,∠CBD
,∠CBD![]() ,AD=1,求CD的長.
,AD=1,求CD的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小趙和小王約定在早上7:00至7:15之間到某公交站搭乘公交車去上學,已知在這段時間內,共有2班公交車到達該站,到站的時間分別為7:05,7:15,如果他們約定見車就搭乘,則小趙和小王恰好能搭乘同一班公交車去上學的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某景區修建一棟復古建筑,其窗戶設計如圖所示.圓![]() 的圓心與矩形
的圓心與矩形![]() 對角線的交點重合,且圓與矩形上下兩邊相切(
對角線的交點重合,且圓與矩形上下兩邊相切(![]() 為上切點),與左右兩邊相交(
為上切點),與左右兩邊相交(![]() ,
,![]() 為其中兩個交點),圖中陰影部分為不透光區域,其余部分為透光區域.已知圓的半徑為1
為其中兩個交點),圖中陰影部分為不透光區域,其余部分為透光區域.已知圓的半徑為1![]() ,且
,且![]() ,設
,設![]() ,透光區域的面積為
,透光區域的面積為![]() .
.
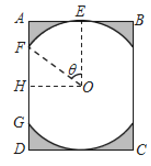
(1)求![]() 關于
關于![]() 的函數關系式,并求出定義域;
的函數關系式,并求出定義域;
(2)根據設計要求,透光區域與矩形窗面的面積比值越大越好.當該比值最大時,求邊![]() 的長度.
的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公園要設計如圖所示的景觀窗格(其結構可以看成矩形在四個角處對稱地截去四個全等的三角形所得,如圖二中所示多邊形![]() ),整體設計方案要求:內部井字形的兩根水平橫軸
),整體設計方案要求:內部井字形的兩根水平橫軸![]() 米,兩根豎軸
米,兩根豎軸![]() 米,記景觀窗格的外框(如圖二實線部分,軸和邊框的粗細忽略不計)總長度為
米,記景觀窗格的外框(如圖二實線部分,軸和邊框的粗細忽略不計)總長度為![]() 米.
米.

(1)若![]() ,且兩根橫軸之間的距離為
,且兩根橫軸之間的距離為![]() 米,求景觀窗格的外框總長度;
米,求景觀窗格的外框總長度;
(2)由于預算經費限制,景觀窗格的外框總長度不超過![]() 米,當景觀窗格的面積(多邊形
米,當景觀窗格的面積(多邊形![]() 的面積)最大時,給出此景觀窗格的設計方案中
的面積)最大時,給出此景觀窗格的設計方案中![]() 的大小與
的大小與![]() 的長度.
的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數y=f(x)的定義域為D,若對任意的x1∈D,總存在x2∈D,使得f(x1)f(x2)=1,則稱函數f(x)具有性質M.下列結論:①函數y=x3﹣x具有性質M;②函數y=3x+5x具有性質M;③若函數y=log8(x+2),x∈[0,t]時具有性質M,則t=510;④若y![]() 具有性質M,則a=5.其中正確結論的序號是_____.
具有性質M,則a=5.其中正確結論的序號是_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com