
【題目】下列命題的說法錯誤的是( )
A.命題“若x2﹣3x+2=0,則 x=1”的逆否命題為:“若x≠1,則x2﹣3x+2≠0”.
B.“x=1”是“x2﹣3x+2=0”的充分必要條件.
C.命題p:“?x∈R,sinx+cosx≤ ![]() ”是真命題
”是真命題
D.若¬(p∧q)為真命題,則p、q至少有一個為假命題.
【答案】B
【解析】解:根據原命題與逆否命題的定義即可知道A正確; 方程x2﹣3x+2=0的根為x=1,或2,
∴x=1能得到x2﹣3x+2=0,而x2﹣3x+2=0得不到x=1,
∴“x=1”是“x2﹣3x+2=0”的充分不必要條件,
即B是錯誤的;
“x∈R,sinx+cosx= ![]() sin(x+
sin(x+ ![]() )≤
)≤ ![]() ”,
”,
故命題p:“x∈R,sinx+cosx≤ ![]() ”是真命題,
”是真命題,
故C正確;
若¬(p∧q)為真命題,則p∧q是假命題,
則p,q至少1個是假命題;
故D正確,
故選:B.
【考點精析】通過靈活運用四種命題,掌握原命題:若P則q; 逆命題:若q則p;否命題:若┑P則┑q;逆否命題:若┑q則┑p即可以解答此題.


科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的準線為
的準線為![]() ,焦點為
,焦點為![]() ,
, ![]() 為坐標原點.
為坐標原點.
(1)求過點![]() ,且與
,且與![]() 相切的圓的方程;
相切的圓的方程;
(2)過![]() 的直線交拋物線
的直線交拋物線![]() 于
于![]() 兩點,
兩點, ![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,求證:直線
,求證:直線![]() 過定點.
過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知 ![]() ,
, ![]() 的夾角為120°,|
的夾角為120°,| ![]() |=2,|
|=2,| ![]() |=3,記|
|=3,記| ![]() =3
=3 ![]() ﹣2
﹣2 ![]() ,
, ![]() =2
=2 ![]() +k
+k ![]() .
.
(1)若 ![]() ⊥
⊥ ![]() ,求實數k的值.
,求實數k的值.
(2)是否存在實數k,使得 ![]() ∥
∥ ![]() ?說明理由.
?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】共享單車入住泉州一周年以來,因其“綠色出行,低碳環保”的理念而備受人們的喜愛,值此周年之際,某機構為了了解共享單車使用者的年齡段,使用頻率、滿意度等三個方面的信息,在全市范圍內發放![]() 份調查問卷,回收到有效問卷
份調查問卷,回收到有效問卷![]() 份,現從中隨機抽取
份,現從中隨機抽取![]() 份,分別對使用者的年齡段、
份,分別對使用者的年齡段、![]() ~
~![]() 歲使用者的使用頻率、
歲使用者的使用頻率、![]() ~
~![]() 歲使用者的滿意度進行匯總,得到如下三個表格:
歲使用者的滿意度進行匯總,得到如下三個表格:
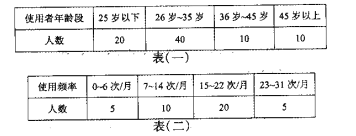
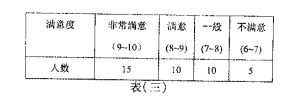
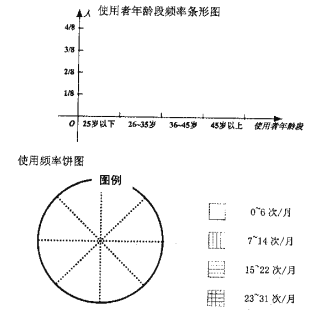
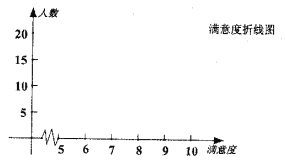
(Ⅰ)依據上述表格完成下列三個統計圖形:
(Ⅱ)某城區現有常住人口![]() 萬,請用樣本估計總體的思想,試估計年齡在
萬,請用樣本估計總體的思想,試估計年齡在![]() 歲~
歲~![]() 歲之間,每月使用共享單車在
歲之間,每月使用共享單車在![]() ~
~![]() 次的人數.
次的人數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=Asin(ωx+φ) ![]() 部分圖象如圖所示.
部分圖象如圖所示.
(Ⅰ)求f(x)的最小正周期及解析式;
(Ⅱ)設g(x)=f(x)﹣cos2x,求函數g(x)在區間 ![]() 上的最大值和最小值.
上的最大值和最小值.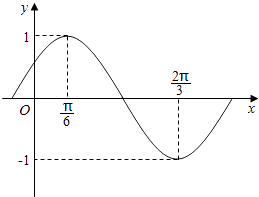
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等差數列{an}的公差為d,前n項和為Sn , 等比數列{bn}的公比為q,已知b1=a1 , b2=2,q=d,S10=100.
(1)求數列{an},{bn}的通項公式
(2)當d>1時,記cn= ![]() ,求數列{cn}的前n項和Tn .
,求數列{cn}的前n項和Tn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com