
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)若![]() ,直線
,直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,求
兩點,求![]() ;
;
(2)若![]() ,求曲線
,求曲線![]() 上的點到直線
上的點到直線![]() 的距離的最小值.
的距離的最小值.
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點為
的左右焦點為![]() ,過
,過![]() (M不過橢圓的頂點和中心)且斜率為k直線l交橢圓于
(M不過橢圓的頂點和中心)且斜率為k直線l交橢圓于![]() 兩點,與y軸交于點N,且
兩點,與y軸交于點N,且![]() .
.
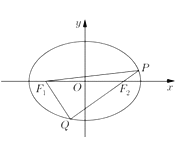
(1)若直線l過點![]() ,求
,求![]() 的周長;
的周長;
(2)若直線l過點![]() ,求線段
,求線段![]() 的中點R的軌跡方程;
的中點R的軌跡方程;
(3)求證:![]() 為定值,并求出此定值.
為定值,并求出此定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某花圃為提高某品種花苗質量,開展技術創新活動,在![]() ,
,![]() 實驗地分別用甲、乙方法培育該品種花苗.為觀測其生長情況,分別在
實驗地分別用甲、乙方法培育該品種花苗.為觀測其生長情況,分別在![]() ,
,![]() 試驗地隨機抽選各
試驗地隨機抽選各![]() 株,對每株進行綜合評分(評分的高低反映花苗品質的高低),將每株所得的綜合評分制成如圖所示的頻率分布直方圖:
株,對每株進行綜合評分(評分的高低反映花苗品質的高低),將每株所得的綜合評分制成如圖所示的頻率分布直方圖:
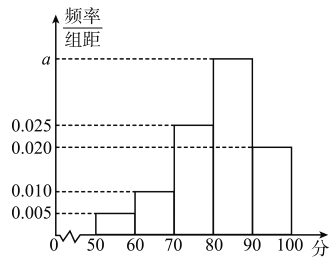
(1)求圖中![]() 的值,并求綜合評分的中位數;
的值,并求綜合評分的中位數;
(2)記綜合評分為![]() 及以上的花苗為優質花苗.填寫下面的列聯表,并判斷是否有
及以上的花苗為優質花苗.填寫下面的列聯表,并判斷是否有![]() 的把握認為優質花苗與培育方法有關.
的把握認為優質花苗與培育方法有關.
優質花苗 | 非優質花苗 | 合計 | |
甲培育法 |
| ||
乙培育法 |
| ||
合計 |
附:下面的臨界值表僅供參考.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(參考公式: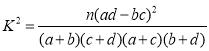 ,其中
,其中![]() .)
.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() ,記集合
,記集合![]() .
.
(1)對于數列![]() ,寫出集合
,寫出集合![]() ;
;
(2)若![]() ,是否存在
,是否存在![]() ,使得
,使得![]() ?若存在,求出一組符合條件的
?若存在,求出一組符合條件的![]() ;若不存在,說明理由.
;若不存在,說明理由.
(3)若![]() ,把集合
,把集合![]() 中的元素從小到大排列,得到的新數列為
中的元素從小到大排列,得到的新數列為![]() ,若
,若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知對于任意![]() ,函數
,函數![]()
![]() 與
與![]()
![]() 的圖像在
的圖像在![]() 上都有三個不同交點.
上都有三個不同交點.
(1)寫出![]() 的解析式,并求函數的最大值及此時的x的取值;
的解析式,并求函數的最大值及此時的x的取值;
(2)若函數![]() 在
在![]() 和
和![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,且
上單調遞減,且![]() ,求
,求![]() 的所有可能值.
的所有可能值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】環保部門要對所有的新車模型進行廣泛測試,以確定它的行車里程的等級,下表是對100輛新車模型在一個耗油單位內行車里程(單位:公里)的測試結果.
分組 | 頻數 |
| 6 |
| 10 |
| 20 |
| 30 |
| 18 |
| 12 |
| 4 |
(1)做出上述測試結果的頻率分布直方圖,并指出其中位數落在哪一組;
(2)用分層抽樣的方法從行車里程在區間![]() 與
與![]() 的新車模型中任取5輛,并從這5輛中隨機抽取2輛,求其中恰有一個新車模型行車里程在
的新車模型中任取5輛,并從這5輛中隨機抽取2輛,求其中恰有一個新車模型行車里程在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 上的一點
上的一點![]() 到其左頂點
到其左頂點![]() 的距離為
的距離為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(
兩點(![]() 與點
與點![]() 不重合),若以
不重合),若以![]() 為直徑的圓經過點
為直徑的圓經過點![]() ,試證明:直線
,試證明:直線![]() 過定點.
過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】黨中央、國務院歷來高度重視青少年的健康成長.“少年強則國強”,青少年身心健康、體魄強健、意志堅強、充滿活力,是一個民族旺盛生命力的體現,是社會文明進步的標志,是國家綜合實力的重要方面.全面實施《國家學生體質健康標準》,把健康素質作為評價學生全面健康發展的重要指標,是新時代的要求.《國家學生體質健康標準》有一項指標是學生體質指數(![]() ),其計算公式為:
),其計算公式為: ,當
,當![]() 時,認為“超重”,應加強鍛煉以改善
時,認為“超重”,應加強鍛煉以改善![]() .某高中高一、高二年級學生共2000人,人數分布如表(a).為了解這2000名學生的
.某高中高一、高二年級學生共2000人,人數分布如表(a).為了解這2000名學生的![]() 指數情況,從中隨機抽取容量為160的一個樣本.
指數情況,從中隨機抽取容量為160的一個樣本.
表(a)
性別 年級 | 男生 | 女生 | 合計 |
高一年級 | 550 | 650 | 1200 |
高二年級 | 425 | 375 | 800 |
合計 | 975 | 1025 | 2000 |
(1)為了使抽取的160個學生更具代表性,宜采取分層抽樣,試給出一個合理的分層抽樣方案,并確定每層應抽取出的學生人數;
(2)分析這160個學生的![]() 值,統計出“超重”的學生人數分布如表(b).
值,統計出“超重”的學生人數分布如表(b).
表(b)
性別 年級 | 男生 | 女生 |
高一年級 | 4 | 6 |
高二年級 | 2 | 4 |
(ⅰ)試估計這2000名學生中“超重”的學生數;
(ⅱ)對于該校的2000名學生,應用獨立性檢驗的知識,可分析出性別變量與年級變量哪一個與“是否超重”的關聯性更強.應用卡方檢驗,可依次得到![]() 的觀測值
的觀測值![]() ,
,![]() ,試判斷
,試判斷![]() 與
與![]() 的大小關系.(只需寫出結論)
的大小關系.(只需寫出結論)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com