
分析 (1)依題意,可得數列{an+1}是以2為首項,2為公比的等比數列,于是可求得數列{an}的通項公式an和Sn;
(2)化簡bn=(an+1)log${\;}_{\frac{1}{2}}$(an+1)為bn=-n•2n,利用錯位相減法可求得數列{bn}的前n項和為Tn=(1-n)2n+1-2,代入Tn+n•2n+1>50可得使之成立的正整數n的最小值.
解答 解:(1)∵點{an,an+1)在直線y=2x+1上,
∴an+1=2an+1,即an+1+1=2(an+1),又a1=1,a1+1=2,
∴數列{an+1}是以2為首項,2為公比的等比數列,
∴an+1=2n,
∴an=2n-1.
Sn=a1+a2+…an=(21+22+…+2n)-n=$\frac{2(1{-2}^{n})}{1-2}$-n=2n+1-n-2.
(2)∵bn=(an+1)log${\;}_{\frac{1}{2}}$(an+1)=2nlog${\;}_{\frac{1}{2}}$2n=-n•2n,
∴-Tn=1•21+2•22+…+n•2n,①
-2Tn=1•22+2•23+…+…+(n-1)•2n+n•2n+1,②
①-②得:Tn=21+22+…+2n-n•2n+1=2n+1-2-n•2n+1=(1-n)2n+1-2.
要使Tn+n•2n+1>50成立,即(1-n+n)2n+1-2=2n+1-2>50成立,
∵25=32<52,26=64>52,即當n+1≥6,n≥5時,2n+1-2>50恒成立,
∴使Tn+n•2n+1>50成立的正整數n的最小值為5.
點評 本題考查數列的遞推式,考查等比數列的關系的確定與通項公式的求法,突出考查錯位相減法求和的應用,考查轉化思想與運算能力,屬于中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{6}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | p |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(0)+f(2)<2f(1) | B. | f(0)+f(2)≤2f(1) | C. | f(0)+f(2)≥2f(1) | D. | f(0)+f(2)>2f(1) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
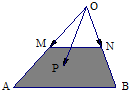 如圖所示,在△OAB中,M、N分別是OA、OB的中點,點P在梯形ABNM區域(含邊界)上移動,且$\overrightarrow{OP}=x\overrightarrow{OM}+y\overrightarrow{ON}$,則4x+3y的取值范圍是[3,8].
如圖所示,在△OAB中,M、N分別是OA、OB的中點,點P在梯形ABNM區域(含邊界)上移動,且$\overrightarrow{OP}=x\overrightarrow{OM}+y\overrightarrow{ON}$,則4x+3y的取值范圍是[3,8].查看答案和解析>>
科目:高中數學 來源: 題型:解答題
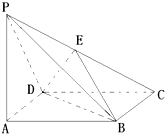 如圖,四棱錐P-ABCD的底面是邊長為a的正方形,PA⊥平面ABCD,PA=a,E為CP中點,
如圖,四棱錐P-ABCD的底面是邊長為a的正方形,PA⊥平面ABCD,PA=a,E為CP中點,查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①④ | B. | ②③ | C. | ①②③ | D. | ④ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com