
分析 橢圓左焦點設為F1,連接MF1.利用橢圓的定義以及在三角形中,兩邊之差總小于第三邊,當A、M、F1成一直線時,|MA|-|MF1|最大,求解即可.利用|MA|+|MF2|=|MA|+6-|MF1|=10-(|MF1|-|MA|)≥6-|AF1|,即可得出其最小值.
解答 解:由橢圓$\frac{x^2}{9}$+$\frac{y^2}{8}$=1的焦點在x軸上,a=3,b=2$\sqrt{2}$,c=1,
左焦點為F1(-1,0),連接MF1.
由橢圓的定義可知:|MF1|+|MF|=2a,
|MA|+|MF|=|MA|+2a-|MF1|=6+|MA|-|MF1|.
即|MA|-|MF1|最大時,|MA|+|MF2|最大.
在△AMF1中,兩邊之差總小于第三邊,所以當A、M、F1成一直線時,|MA|-|MF1|最大,
|MA|-|MF1|=|AF1|=$\sqrt{(1+1)^{2}+(2-0)^{2}}$=2$\sqrt{2}$.
∴|MA|+|MF2|的最大值是6+2$\sqrt{2}$.
∴|MA|+|MF2|=|MA|+6-|MF1|=6-(|MF1|-|MA|)≥10-|AF1|=6-2$\sqrt{2}$,
∴|MA|+|MF|的取值范圍(6-2$\sqrt{2}$,6+2$\sqrt{2}$),
故答案為:(6-2$\sqrt{2}$,6+2$\sqrt{2}$).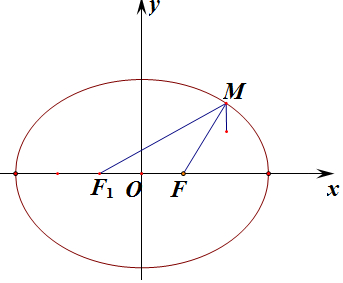
點評 本題主要考查圓錐曲線的定義的應用,在解決涉及到圓錐曲線上的點與焦點之間的關系的問題中,考查數形結合思想的應用,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
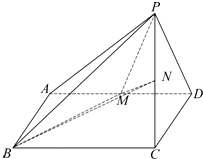 四棱錐P-ABCD中,PC=AB=1,BC=2,∠ABC=60°,底面ABCD為平行四邊形,PC⊥平面ABCD,點M,N分別為AD,PC的中點.
四棱錐P-ABCD中,PC=AB=1,BC=2,∠ABC=60°,底面ABCD為平行四邊形,PC⊥平面ABCD,點M,N分別為AD,PC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{5}$或-$\sqrt{5}$ | B. | $\sqrt{5}$或0 | C. | -$\sqrt{5}$或0 | D. | 0或$\sqrt{5}$或-$\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{17}{2}$ | B. | $\frac{19}{2}$ | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com