
分析 (1)首先函數的定義域為(0,+∞),然后求出函數的導數f′(x),將f′(x)變形后,再結合x>0和b>$\frac{1}{2}$得f′(x)>0,可得函數f(x)在定義域(0,+∞)上單調遞增;
(2)方程f′(x)=0在(0,+∞)有兩個不相等的實數根時,函數有極值.然后利用根的判別式算得當b<$\frac{1}{2}$時,函數存在極值點,最后根據b≤0和0<b<$\frac{1}{2}$兩種情況分別得出函數的極值點.
解答 解:(1)f′(x)=-2(x-1)-$\frac{b}{x}$=-$\frac{{2(x-\frac{1}{2})}^{2}+b-\frac{1}{2}}{x}$,
當b>$\frac{1}{2}$時,f′(x)<0,
函數f(x)在定義域(0,+∞)遞減;
(2)①由(1),b>$\frac{1}{2}$時,函數f(x)無極值點,
②b=$\frac{1}{2}$時,有2個相同的解x=$\frac{1}{2}$,
∴b=$\frac{1}{2}$時,函數f(x)在(-1,+∞)無極值點,
③b<$\frac{1}{2}$時,f′(x)=0有兩個不同的解,
x1=$\frac{1}{2}$-$\frac{\sqrt{1-2b}}{2}$,x2=$\frac{1}{2}$+$\frac{\sqrt{1-2b}}{2}$,
∴(i)b≤0時,x1=$\frac{1}{2}$-$\frac{\sqrt{1-2b}}{2}$≤0∉(0,+∞),舍去,
而x2=$\frac{1}{2}$+$\frac{\sqrt{1-2b}}{2}$≥1∈(0,+∞),
此時f′(x),f(x)隨x在定義域上的變化情況如下表:
| x | (0,x2) | x2 | (x2,+∞) |
| f′(x) | + | 0 | - |
| f(x) | 遞增 | 極大值 | 遞減 |
| x | (0,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | 遞減 | 極小值 | 遞增 | 極大值 | 遞減 |
點評 本題考查了利用導數研究函數的單調性和含有字母參數的函數極值的討論,屬于中檔題.


 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | -8 | B. | -4 | C. | -2 | D. | 0 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 單位向量都相等 | |
| B. | 長度相等且方向相反的兩個向量不一定是共線向量 | |
| C. | 若$\overrightarrow a$,$\overrightarrow b$滿足$|{\overrightarrow a}|$>$|{\overrightarrow b}|$且$\overrightarrow a$與$\overrightarrow b$同向,則$\overrightarrow a$>$\overrightarrow b$ | |
| D. | 對于任意向量$\overrightarrow a$,$\overrightarrow b$,必有$|{\overrightarrow a+\overrightarrow b}|$≤$|{\overrightarrow a}|$+$|{\overrightarrow b}|$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
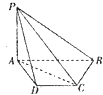 如圖所示,四棱錐P-ABCD的底面為等腰梯形,AB∥DC,AB=2AD,若PA⊥平面ABCD,∠ABC=60°
如圖所示,四棱錐P-ABCD的底面為等腰梯形,AB∥DC,AB=2AD,若PA⊥平面ABCD,∠ABC=60°查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{20}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 3 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2sin5 | B. | -2cos5 | C. | 2sin5 | D. | 2cos5 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com