
分析 由a>0,b>0,且滿足3a+b=a2+ab,可得b=$\frac{{a}^{2}-3a}{1-a}$>0,解得1<a<3.則2a+b=2a+$\frac{{a}^{2}-3a}{1-a}$=a-1+$\frac{2}{a-1}$+3,利用基本不等式的性質即可得出.
解答 解:由a>0,b>0,且滿足3a+b=a2+ab,∴b=$\frac{{a}^{2}-3a}{1-a}$>0,解得1<a<3.
則2a+b=2a+$\frac{{a}^{2}-3a}{1-a}$=a-1+$\frac{2}{a-1}$+3≥2$\sqrt{(a-1)•\frac{2}{a-1}}$+3=2$\sqrt{2}$+3,當且僅當a=1+$\sqrt{2}$,b=1時取等號.
故答案為:3+2$\sqrt{2}$.
點評 本題考查了基本不等式的性質,考查了推理能力與計算能力,屬于中檔題.


 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2個 | B. | 3個 | C. | 4個 | D. | 5個 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
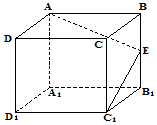 如圖,正方體ABCD-A1B1C1D1中,E為棱BB1的中點,用過點A、E、C1的平面截去該正方體的下半部分,則剩余幾何體的正視圖(也稱主視圖)是( )
如圖,正方體ABCD-A1B1C1D1中,E為棱BB1的中點,用過點A、E、C1的平面截去該正方體的下半部分,則剩余幾何體的正視圖(也稱主視圖)是( )| A. | 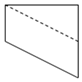 | B. | 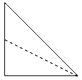 | C. | 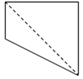 | D. | 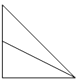 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com