
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點 .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過橢圓![]() 左焦點的直線
左焦點的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,直線
兩點,直線![]() 過坐標原點且直線
過坐標原點且直線![]() 與
與![]() 的斜率互為相反數,直線
的斜率互為相反數,直線![]() 與橢圓交于
與橢圓交于![]() 兩點且均不與點
兩點且均不與點![]() 重合,設直線
重合,設直線![]() 的斜率為
的斜率為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() .證明:
.證明: ![]() 為定值.
為定值.
科目:高中數學 來源: 題型:
【題目】四棱錐![]() 的底面
的底面![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 為正三角形.
為正三角形.
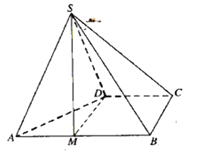
(1)點![]() 為棱
為棱![]() 上一點,若
上一點,若![]() 平面
平面![]() ,
,![]() ,求實數
,求實數![]() 的值;
的值;
(2)求點B到平面SAD的距離.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)由![]() 平面
平面![]() ,可證
,可證![]() ,進而證得四邊形
,進而證得四邊形![]() 為平行四邊形,根據
為平行四邊形,根據![]() ,可得
,可得![]() ;
;
(2)利用等體積法![]() 可求點
可求點![]() 到平面
到平面![]() 的距離.
的距離.
試題解析:((1)因為![]() 平面SDM,
平面SDM,
![]()
![]() 平面ABCD,
平面ABCD,
平面SDM ![]() 平面ABCD=DM,
平面ABCD=DM,
所以![]() ,
,
因為![]() ,所以四邊形BCDM為平行四邊形,又
,所以四邊形BCDM為平行四邊形,又![]() ,所以M為AB的中點.
,所以M為AB的中點.
因為![]() ,
,
![]() .
.

(2)因為![]()
![]() ,
, ![]()
![]() ,
,
所以![]() 平面
平面![]() ,
,
又因為![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
在平面![]() 內過點
內過點![]() 作
作![]() 直線
直線![]() 于點
于點![]() ,則
,則![]() 平面
平面![]() ,
,
在![]() 和
和![]() 中,
中,
因為![]() ,所以
,所以![]() ,
,
又由題知![]() ,
,
所以![]() ,
,
由已知求得![]() ,所以
,所以![]() ,
,
連接BD,則![]() ,
,
又求得![]() 的面積為
的面積為![]() ,
,
所以由![]() 點B 到平面
點B 到平面![]() 的距離為
的距離為![]() .
.
【題型】解答題
【結束】
19
【題目】小明在石家莊市某物流派送公司找到了一份派送員的工作,該公司給出了兩種日薪薪酬方案.甲方案:底薪100元,每派送一單獎勵1元;乙方案:底薪140元,每日前55單沒有獎勵,超過55單的部分每單獎勵12元.
(1)請分別求出甲、乙兩種薪酬方案中日薪![]() (單位:元)與送貨單數
(單位:元)與送貨單數![]() 的函數關系式;
的函數關系式;
(2)根據該公司所有派送員100天的派送記錄,發現派送員的日平均派送單數與天數滿足以下表格:
日均派送單數 | 52 | 54 | 56 | 58 | 60 |
頻數(天) | 20 | 30 | 20 | 20 | 10 |
回答下列問題:
①根據以上數據,設每名派送員的日薪為![]() (單位:元),試分別求出這100天中甲、乙兩種方案的日薪
(單位:元),試分別求出這100天中甲、乙兩種方案的日薪![]() 平均數及方差;
平均數及方差;
②結合①中的數據,根據統計學的思想,幫助小明分析,他選擇哪種薪酬方案比較合適,并說明你的理由.
(參考數據: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等比數列![]() 的公比
的公比![]() ,前
,前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() .
.![]() ,
,![]() ,
,![]() 分別是一個等差數列的第1項,第2項,第5項.
分別是一個等差數列的第1項,第2項,第5項.
(1)求數列![]() 的通項公式;
的通項公式;
(2)設![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)若![]() ,
,![]() 的前
的前![]() 項和為
項和為![]() ,且對任意的
,且對任意的![]() 滿足
滿足![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,曲線
,曲線![]() 在
在![]() 處的切線經過點
處的切線經過點![]() .
.
(1)證明: ![]() ;
;
(2)若當![]() 時,
時, 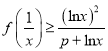 ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)證明見解析;(2) ![]() .
.
【解析】試題分析:(1)先根據導數幾何意義得切線斜率為![]() ,再根據切線過點
,再根據切線過點![]() ,解得
,解得![]() 導數可得導函數零點,列表分析導函數符號變號規律可得函數單調性,根據函數單調性可得函數最小值為0,即得結論,(2)先化簡不等式為
導數可得導函數零點,列表分析導函數符號變號規律可得函數單調性,根據函數單調性可得函數最小值為0,即得結論,(2)先化簡不等式為![]() ,分離得
,分離得![]() ,再利用導數求函數
,再利用導數求函數![]() 單調性,利用羅伯特法則求最大值,即得
單調性,利用羅伯特法則求最大值,即得![]() 的取值范圍.
的取值范圍.
試題解析:(1)曲線![]() 在
在![]() 處的切線為
處的切線為![]() ,即
,即![]()
由題意得![]() ,解得
,解得![]()
所以![]()
從而![]()
因為當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() .
.
所以![]() 在區間
在區間![]() 上是減函數,區間
上是減函數,區間![]() 上是增函數,
上是增函數,
從而![]() .
.
(2)由題意知,當![]() 時,
時, ![]() ,所以
,所以![]()
從而當![]() 時,
時, ![]() ,
,
由題意知 ,即
,即![]() ,其中
,其中![]()
設![]() ,其中
,其中![]()
設![]() ,即
,即![]() ,其中
,其中![]()
則![]() ,其中
,其中![]()
(1)當![]() 時,因為
時,因為![]() 時,
時, ![]() ,所以
,所以![]() 是增函數
是增函數
從而當![]() 時,
時, ![]() ,
,
所以![]() 是增函數,從而
是增函數,從而![]() .
.
故當![]() 時符合題意.
時符合題意.
(2)當![]() 時,因為
時,因為![]() 時,
時, ![]() ,
,
所以![]() 在區間
在區間![]() 上是減函數
上是減函數
從而當![]() 時,
時, ![]()
所以![]() 在
在![]() 上是減函數,從而
上是減函數,從而![]()
故當![]() 時不符合題意.
時不符合題意.
(3)當![]() 時,因為
時,因為![]() 時,
時, ![]() ,所以
,所以![]() 是減函數
是減函數
從而當![]() 時,
時, ![]()
所以![]() 是減函數,從而
是減函數,從而![]()
故當![]() 時不符合題意
時不符合題意
綜上![]() 的取值范圍是
的取值范圍是![]() .
.
【題型】解答題
【結束】
22
【題目】在直角坐標坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),曲線
為參數),曲線![]() :
: ![]() .以
.以![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸,與直角坐標系
軸的非負半軸為極軸,與直角坐標系![]() 取相同的長度單位,建立極坐標系.
取相同的長度單位,建立極坐標系.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)射線![]() (
(![]() )與曲線
)與曲線![]() 的異于極點的交點為
的異于極點的交點為![]() ,與曲線
,與曲線![]() 的交點為
的交點為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中,選項正確的是( )
A. 在回歸直線![]() 中,變量
中,變量![]() 時,變量
時,變量![]() 的值一定是15
的值一定是15
B. 兩個變量相關性越強,則相關系數![]() 就越接近于1
就越接近于1
C. 在殘差圖中,殘差點比較均勻落在水平的帶狀區域中即可說明選用的模型比較合適,與帶狀區域的寬度無關
D. 若某商品的銷售量![]() (件)與銷售價格
(件)與銷售價格![]() (元/件)存在線性回歸方程為
(元/件)存在線性回歸方程為![]() ,當銷售價格為10元時,銷售量為100件左右
,當銷售價格為10元時,銷售量為100件左右
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的部分圖象如圖所示,則下列判斷正確的是( )
的部分圖象如圖所示,則下列判斷正確的是( )
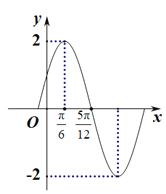
A. 函數的圖象關于點![]() 對稱
對稱
B. 函數的圖象關于直線![]() 對稱
對稱
C. 函數![]() 的最小正周期為
的最小正周期為![]()
D. 當![]() 時,函數
時,函數![]() 的圖象與直線
的圖象與直線![]() 圍成的封閉圖形面積為
圍成的封閉圖形面積為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,
中, ![]() ,且
,且![]() 平面
平面![]() ,
, ![]() 為棱
為棱![]() 的中點.
的中點.

(1)求證: ![]() ∥平面
∥平面![]() ;
;
(2)求證:平面![]() 平面
平面![]() ;
;
(3)當四面體![]() 的體積最大時,判斷直線
的體積最大時,判斷直線![]() 與直線
與直線![]() 是否垂直,并說明理由.
是否垂直,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com