
| 工作日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| 限行車牌尾號 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
分析 (1)記事件A“該公司在星期一至少有2輛車出車”,利用獨立重復試驗的概率乘法公式,求解即可;
(2)X的可能取值為0,1,2,3,4,5,求出對應的概率,寫出分布列,計算數學期望值.
解答 解:(1)記事件A“該公司在星期一至少有2輛車出車”,
則P(A)=1-${(\frac{1}{2})}^{3}$•${(\frac{1}{3})}^{2}$-${C}_{3}^{1}$•${(\frac{1}{2})}^{3}$•${(\frac{1}{3})}^{2}$-${C}_{2}^{1}$•${(\frac{1}{2})}^{3}$•$\frac{1}{3}$•$\frac{2}{3}$
=1-$\frac{1}{72}$-$\frac{3}{72}$-$\frac{4}{72}$
=$\frac{8}{9}$;
(2)根據題意,X的可能取值為0,1,2,3,4,5;
則P(X=0)=${(\frac{1}{3})}^{2}$•${(\frac{1}{2})}^{3}$=$\frac{1}{72}$,
P(X=1)=${C}_{2}^{1}$•$\frac{2}{3}$•$\frac{1}{3}$•${(\frac{1}{2})}^{3}$+${(\frac{1}{3})}^{2}$•${C}_{3}^{1}$•${(\frac{1}{2})}^{3}$=$\frac{7}{72}$,
P(X=2)=${(\frac{2}{3})}^{2}$•${(\frac{1}{2})}^{3}$+${C}_{2}^{1}$•$\frac{2}{3}$•$\frac{1}{3}$•${C}_{3}^{1}$•${(\frac{1}{2})}^{3}$+${(\frac{1}{3})}^{2}$•${C}_{3}^{2}$•${(\frac{1}{2})}^{3}$=$\frac{19}{72}$,
P(X=3)=${(\frac{2}{3})}^{2}$•${C}_{3}^{1}$•${(\frac{1}{2})}^{3}$+${C}_{2}^{1}$•$\frac{2}{3}$•$\frac{1}{3}$•${C}_{3}^{2}$•${(\frac{1}{2})}^{3}$+${(\frac{1}{3})}^{2}$•${(\frac{1}{2})}^{3}$=$\frac{25}{72}$,
P(X=4)=${(\frac{2}{3})}^{2}$•${C}_{3}^{2}$•${(\frac{1}{2})}^{3}$+${C}_{2}^{1}$•$\frac{2}{3}$•$\frac{1}{3}$•${(\frac{1}{2})}^{3}$=$\frac{16}{72}$,
P(X=5)=${(\frac{2}{3})}^{2}$•${(\frac{1}{2})}^{3}$=$\frac{4}{72}$;
∴隨機變量X的分布列為:
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{1}{72}$ | $\frac{7}{72}$ | $\frac{19}{72}$ | $\frac{25}{72}$ | $\frac{16}{72}$ | $\frac{4}{72}$ |
點評 本題考查了獨立重復試驗的概率求法問題,也考查了離散型隨機變量的分布列與數學期望的計算問題,是中檔題.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
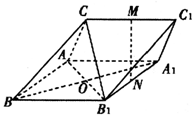 如圖,三棱柱ABC-A1B1Cl中,M,N分別為CC1,A1B1的中點.CA⊥CB1,CA=CB1,BA=BC=BB1.
如圖,三棱柱ABC-A1B1Cl中,M,N分別為CC1,A1B1的中點.CA⊥CB1,CA=CB1,BA=BC=BB1.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
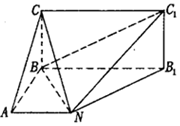 如圖,已知矩形BB1C1C所在平面與底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.
如圖,已知矩形BB1C1C所在平面與底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com