

分析 首先由幾何體的三視圖還原幾何體,然后求體積.其外接球,與以俯視圖為底面,以4為高的直三棱柱的外接球相同,進而可得該幾何體外接球的體積.
解答 解:由已知三視圖得該幾何體是以底面邊長為2的正方形,高為$\sqrt{3}$的四棱錐,
所以其體積為$\frac{1}{3}×{2}^{2}×\sqrt{3}$=$\frac{4\sqrt{3}}{3}$;
其外接球,與以俯視圖為底面,以2為高的直三棱柱的外接球相同,
如圖所示:
由題意可得底面外接圓的半徑為:r=$\frac{2\sqrt{3}}{3}$,
由棱柱高為2,可得球心距為1,
故外接球半徑為:R=$\sqrt{\frac{4}{3}+1}$=$\sqrt{\frac{7}{3}}$,
故外接球的體積V=$\frac{4}{3}$πR3=$\frac{28\sqrt{21}}{27}$π.
故答案為$\frac{4\sqrt{3}}{3}$;$\frac{28\sqrt{21}}{27}$π.
點評 本題考查的知識要點:三視圖和立體圖之間的轉換,幾何體的體積公式的應用,主要考查學生的空間想象能力和應用能力.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
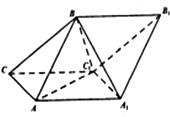 如圖,斜三棱柱ABC-A1B1C1的側面AA1C1C是菱形,側面ABB1A1⊥側面AA1C1C,A1B=AB=AA1=2,△AA1C1的面積為$\sqrt{3}$,且∠AA1C1為銳角.
如圖,斜三棱柱ABC-A1B1C1的側面AA1C1C是菱形,側面ABB1A1⊥側面AA1C1C,A1B=AB=AA1=2,△AA1C1的面積為$\sqrt{3}$,且∠AA1C1為銳角.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源:2017屆安徽合肥一中高三上學期月考一數學(文)試卷(解析版) 題型:解答題
已知函數 .
.
(1)若函數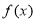 在
在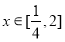 內單調遞減,求實數
內單調遞減,求實數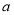 的取值范圍;
的取值范圍;
(2)當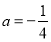 時,關于
時,關于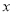 的方程
的方程 在
在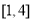 上恰有兩個不相等的實數根,求實數
上恰有兩個不相等的實數根,求實數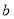 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com