
【題目】在平面直角坐標系中,已知點![]() 和
和![]() ,圓
,圓![]() 是以
是以![]() 為圓心,半徑為
為圓心,半徑為![]() 的圓,點
的圓,點![]() 是圓
是圓![]() 上任意一點,線段
上任意一點,線段![]() 的垂直平分線
的垂直平分線![]() 和半徑
和半徑![]() 所在的直線交于點
所在的直線交于點![]() .
.
(1)當點![]() 在圓上運動時,求點
在圓上運動時,求點![]() 的軌跡方程
的軌跡方程![]() ;
;
(2)已知![]() ,
,![]() 是曲線
是曲線![]() 上的兩點,若曲線
上的兩點,若曲線![]() 上存在點
上存在點![]() ,滿足
,滿足![]() (
(![]() 為坐標原點),求實數
為坐標原點),求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(Ⅰ)連結QF,由已知條件推導出|QP|=|QF|,從而得到|QE|+|QF|=PE=2![]() ,由此推導出點Q的軌跡方程T是以E(﹣1,0)和F(1,0)為焦點的橢圓,進而能求出點Q的軌跡方程T.
,由此推導出點Q的軌跡方程T是以E(﹣1,0)和F(1,0)為焦點的橢圓,進而能求出點Q的軌跡方程T.
(Ⅱ)設直線l的方程為y=kx+m,把y=kx+m代入橢圓![]() ,得(1+2k2)x2+4kx+2m2﹣2=0,分m=0和m≠0兩種情況進行討論,能求出實數λ的取值范圍.
,得(1+2k2)x2+4kx+2m2﹣2=0,分m=0和m≠0兩種情況進行討論,能求出實數λ的取值范圍.
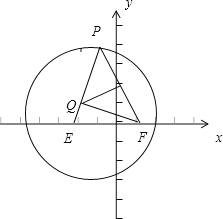
解:(Ⅰ)如圖,連結QF,
∵點E(﹣1,0)和F(1,0),
圓E是以E為圓心,半徑為![]() 的圓,點P是圓E上任意一點,
的圓,點P是圓E上任意一點,
線段FP的垂直平分線l和半徑EP所在的直線交于點Q,
∴|QP|=|QF|,∴|QE|+|QF|=PE=2![]() ,
,
∴點Q的軌跡方程T是以E(﹣1,0)和F(1,0)為焦點的橢圓,
且2a=2![]() ,a
,a![]() ,c=1,∴b=1,
,c=1,∴b=1,
∴點Q的軌跡方程T:![]() .
.
(Ⅱ)設經過點M、N的直線為l,由題意和l的斜率存在,
設直線l的方程為y=kx+m,
把y=kx+m代入橢圓![]() ,
,
整理,得(1+2k2)x2+4kx+2m2﹣2=0,
設M(x1,y1),N(x2,y2),P(x0,y0),
則![]() ,x1x2
,x1x2![]() ,
,
∴y1+y2=k(x1+x2)+2m![]() ,
,
①當m=0時,點M,N關于原點對稱,則λ=0;
②當m≠0時,點M,N不關于原點對稱,則λ≠0,
∵![]() ,
,
∴x1+x2=λx0,y1+y2=λy0,
∴ ,y0
,y0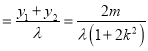 ,
,
∵點P在![]() 上,
上,
∴[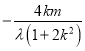 ]2+2[
]2+2[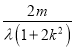 ]2=2,
]2=2,
化簡,得4m2(1+2k2)=λ2(1+k2)2,
∵1+2k2≠0,∴4m2=λ2(1+2k2),①
又∵△=16k2m2﹣4(1+2k2)(2m2﹣2)
=8(1+2k2﹣m2)>0,
∴1+2k2>m2,②
聯立①②及m≠0,得λ2<4,∴﹣2<λ<2,且λ≠0.
綜上所述,實數λ的取值范圍是(﹣2,2).


 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案 新思維小冠軍100分作業本系列答案
新思維小冠軍100分作業本系列答案科目:高中數學 來源: 題型:
【題目】如圖,某野生保護區監測中心設置在點![]() 處,正西、正東、正北處有三個監測點
處,正西、正東、正北處有三個監測點![]() ,且
,且![]() ,一名野生動物觀察員在保護區遇險,發出求救信號,三個監測點均收到求救信號,
,一名野生動物觀察員在保護區遇險,發出求救信號,三個監測點均收到求救信號,![]() 點接收到信號的時間比
點接收到信號的時間比![]() 點接收到信號的時間早
點接收到信號的時間早![]() 秒(注:信號每秒傳播
秒(注:信號每秒傳播![]() 千米).
千米).

(1)以![]() 為原點,直線
為原點,直線![]() 為
為![]() 軸建立平面直角坐標系(如題),根據題設條件求觀察員所有可能出現的位置的軌跡方程;
軸建立平面直角坐標系(如題),根據題設條件求觀察員所有可能出現的位置的軌跡方程;
(2)若已知![]() 點與
點與![]() 點接收到信號的時間相同,求觀察員遇險地點坐標,以及與檢測中心
點接收到信號的時間相同,求觀察員遇險地點坐標,以及與檢測中心![]() 的距離;
的距離;
(3)若![]() 點監測點信號失靈,現立即以監測點
點監測點信號失靈,現立即以監測點![]() 為圓心進行“圓形”紅外掃描,為保證有救援希望,掃描半徑
為圓心進行“圓形”紅外掃描,為保證有救援希望,掃描半徑![]() 至少是多少公里?
至少是多少公里?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正整數數列![]() 的前
的前![]() 項和為
項和為![]() ,前
,前![]() 項積
項積![]() ,若
,若![]() ,則稱數列
,則稱數列![]() 為“
為“![]() 數列”.
數列”.
(1)判斷下列數列是否是![]() 數列,并說明理由;①2,2,4,8;②8,24,40,56
數列,并說明理由;①2,2,4,8;②8,24,40,56
(2)若數列![]() 是
是![]() 數列,且
數列,且![]() .求
.求![]() 和
和![]() ;
;
(3)是否存在等差數列是![]() 數列?請闡述理由.
數列?請闡述理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,平面四邊形![]() 中,
中,![]() ,
,![]() 是
是![]() ,
,![]() 中點,
中點,![]() ,
,![]() ,
,![]() ,將
,將![]() 沿對角線
沿對角線![]() 折起至
折起至![]() ,使平面
,使平面![]() 平面
平面![]() ,則四面體
,則四面體![]() 中,下列結論不正確的是( )
中,下列結論不正確的是( )
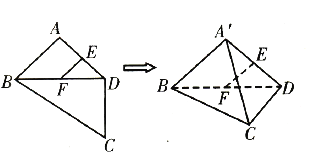
A. ![]() 平面
平面![]()
B. 異面直線![]() 與
與![]() 所成的角為
所成的角為![]()
C. 異面直線![]() 與
與![]() 所成的角為
所成的角為![]()
D. 直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]() ,過其焦點
,過其焦點![]() 作斜率為1的直線交拋物線
作斜率為1的直線交拋物線![]() 于
于![]() ,
,![]() 兩點,且線段
兩點,且線段![]() 的中點的縱坐標為4.
的中點的縱坐標為4.
(1)求拋物線![]() 的標準方程;
的標準方程;
(2)若不過原點![]() 且斜率存在的直線
且斜率存在的直線![]() 與拋物線
與拋物線![]() 相交于
相交于![]() 、
、![]() 兩點,且
兩點,且![]() .求證:直線
.求證:直線![]() 過定點,并求出該定點的坐標.
過定點,并求出該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了解廣告投入對銷售收益的影響,在若干地區各投入4萬元廣告費用,并將各地的銷售收益繪制成頻率分布直方圖(如圖所示).由于工作人員失誤,橫軸的數據丟失,但可以確定橫軸是從0開始計數的.

(1)根據頻率分布直方圖計算圖中各小長方形的寬度;
(2)估計該公司投入4萬元廣告費用之后,對應銷售收益的平均值(以各組的區間中點值代表該組的取值);
(3)該公司按照類似的研究方法,測得另外一些數據,并整理得到下表:
廣告投入x(單位:萬元) | 1 | 2 | 3 | 4 | 5 |
銷售收益y(單位:萬元) | 1 | 3 | 4 | 7 |
表中的數據顯示,x與y之間存在線性相關關系,請將(2)的結果填入上表的空白欄,并計算y關于x的回歸方程.
回歸直線的斜率和截距的最小二乘法估計公式分別為 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() :
:![]() 經過點
經過點![]() .設橢圓
.設橢圓![]() 的左頂點為
的左頂點為![]() ,右焦點為
,右焦點為![]() ,右準線與
,右準線與![]() 軸交于點
軸交于點![]() ,且
,且![]() 為線段
為線段![]() 的中點.
的中點.
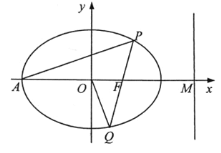
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于另一點
相交于另一點![]() (
(![]() 在
在![]() 軸上方),直線
軸上方),直線![]() 與橢圓
與橢圓![]() 相交于另一點
相交于另一點![]() ,且直線
,且直線![]() 與
與![]() 垂直,求直線
垂直,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校針對校食堂飯菜質量開展問卷調查,提供滿意與不滿意兩種回答,調查結果如下表(單位:人):
學生 | 高一 | 高二 | 高三 |
滿意 | 500 | 600 | 900 |
不滿意 | 300 | 200 | 300 |
(1)求從所有參與調查的人中任選1人是高三學生的概率;
(2)從參與調查的高三學生中,用分層抽樣的方法抽取4人,在這4人中任意選取2人,求這兩人對校食堂飯菜質量都滿意的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分10分)如圖,已知四棱錐![]() 的底面是菱形,對角線
的底面是菱形,對角線![]() 交于點
交于點![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 底面
底面![]() ,設點
,設點![]() 滿足
滿足![]() .
.
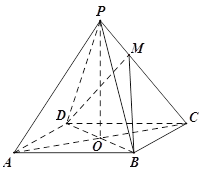
(1)當![]() 時,求直線
時,求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若二面角![]() 的大小為
的大小為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com