
設函數 .
.
(Ⅰ)當 時,求函數
時,求函數 的圖象在點
的圖象在點 處的切線方程;
處的切線方程;
(Ⅱ)已知 ,若函數
,若函數 的圖象總在直線
的圖象總在直線 的下方,求
的下方,求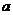 的取值范圍;
的取值范圍;
(Ⅲ)記 為函數
為函數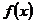 的導函數.若
的導函數.若 ,試問:在區間
,試問:在區間 上是否存在
上是否存在 (
(
 )個正數
)個正數 …
… ,使得
,使得 成立?請證明你的結論.
成立?請證明你的結論.
本題主要考查函數、導數等基礎知識,考查推理論證能力、運算求解能力,考查化歸與轉化思想、分類與整合思想及有限與無限思想.滿分12分.
解:(Ⅰ)當 時,
時,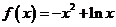 ,
, ,
,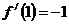 ,
,
所以切線的斜率為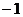 .…………………………………………2分
.…………………………………………2分
又 ,所以切點為
,所以切點為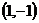 .
.
故所求的切線方程為: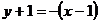 即
即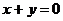 .…………………………………………4分
.…………………………………………4分
(Ⅱ) ,
,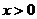 ,
, .………………………6分
.………………………6分
令 ,則
,則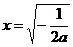 .
.
當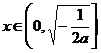 時,
時,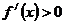 ;當
;當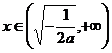 時,
時,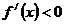 .
.
故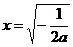 為函數
為函數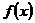 的唯一極大值點,
的唯一極大值點,
所以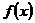 的最大值為
的最大值為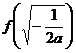 =
=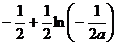 .…………………………………………8分
.…………………………………………8分
由題意有 ,解得
,解得 .
.
所以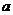 的取值范圍為
的取值范圍為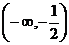 .…………………………………………10分
.…………………………………………10分
(Ⅲ)當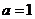 時,
時,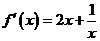 .
記
.
記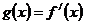 ,其中
,其中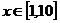 .
.
∵當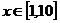 時,
時,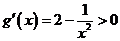 ,∴
,∴ 在
在 上為增函數,
上為增函數,
即 在
在 上為增函數. …………………………………………12分
上為增函數. …………………………………………12分
又 ,
,
所以,對任意的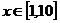 ,總有
,總有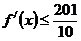 .
.
所以 ,
,
又因為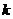
 ,所以
,所以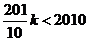 .
.
故在區間 上不存在使得
上不存在使得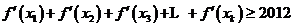 成立的
成立的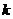 (
(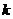
 )個正數
)個正數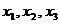 …
… .
………………………14分
.
………………………14分


科目:高中數學 來源: 題型:
(07年寧夏、 海南卷理)(12分)
設函數![]()
(I)若當![]() 時,
時,![]() 取得極值,求
取得極值,求![]() 的值,并討論
的值,并討論![]() 的單調性;
的單調性;
(II)若![]() 存在極值,求
存在極值,求![]() 的取值范圍,并證明所有極值之和大于
的取值范圍,并證明所有極值之和大于![]() .
.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年甘肅省高三(奧班)10月月考理科數學試卷(解析版) 題型:解答題
選修4-5:不等式選講(本小題滿分10分)
設函數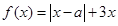 ,其中
,其中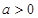 。
。
(Ⅰ)當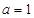 時,求不等式
時,求不等式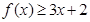 的解集;
的解集;
(Ⅱ)若不等式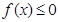 的解集為
的解集為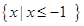 ,求a的值。
,求a的值。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年新人教版高三一輪復習單元測試(8)數學試卷 題型:解答題
(12分)(理)設函數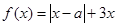 ,其中
,其中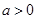 。
。
(Ⅰ)當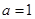 時,求不等式
時,求不等式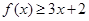 的解集;
的解集;
(Ⅱ)若不等式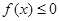 的解集為
的解集為 ,求a的值。
,求a的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com