
| A. | (x+2)2+(y-6)2=1 | B. | (x-6)2+(y+2)2=1 | C. | (x-1)2+(y-3)2=1 | D. | (x+1)2+(y+3)2=1 |
分析 設圓心(-2,6)關于直線x-y+5=0對稱的點的坐標為(m,n),利用垂直以及中點在軸上,求得m,n的值,可得對稱圓的方程.
解答 解:設圓心(-2,6)關于直線x-y+5=0對稱的點的坐標為(m,n),
則由$\left\{\begin{array}{l}{\frac{n-6}{m+2}•1=-1}\\{\frac{m-2}{2}-\frac{n+6}{2}+5=0}\end{array}\right.$求得m=1,n=3,故對稱圓的圓心為(1,3),對稱圓的半徑和原來的圓一樣,
故對稱圓的方程為(x-1)2+(y-3)2=1,
故選C.
點評 本題主要考查直線和圓的位置關系,求一個圓關于直線的對稱圓的方程的方法,關鍵是求出圓心關于直線的對稱點的坐標,屬于基礎題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
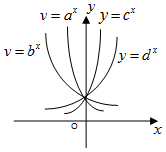 指數函數y=ax、y=bx、y=cx、y=dx在同一坐標系中的圖象如圖所示,則a,b,c,d與1的大小關系為( )
指數函數y=ax、y=bx、y=cx、y=dx在同一坐標系中的圖象如圖所示,則a,b,c,d與1的大小關系為( )| A. | 0<a<b<1<c<d | B. | 0<a<b<1<d<c | C. | 1<a<b<c<d | D. | 0<b<a<1<d<c |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若命題p,¬q都是真命題,則命題“p∧q”為真命題 | |
| B. | 命題“若xy=0,則x=0或y=0”的否命題為“若xy≠0,則x≠0或y≠0” | |
| C. | “x=-1”是“x2-5x-6=0”的必要不充分條件 | |
| D. | 命題“?x∈R,2x>0”的否定是“?x0∈R,2${\;}^{{x}_{0}}$≤0” |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com