Question

平面內有向量=(1,7)，=(5,1)，=(2,1)，點X為直線OP上的一個動點.

(1)當·取最小值時，求的坐標；

(2)當點X滿足(1)的條件和結論時，求cos∠AXB的值.

Answer 1

解：(1)設=(x,y),∵點X在直線OP上，

    ∴向量與共線.

    又=(2,1),∵x·1-y·2=0,即x=2y,∴=(2y,y).

    又=-=(1,7)-(2y,y),

    ∴=(1-2y,7-y).

    同理,=-=(5-2y,1-y).

    于是,·=(1-2y)(5-2y)+(7-y)(1-y)=4y²-12y+5+y²-8y+7=5y²-20y+12

    =5(y-2)²-8.

    由二次函數的知識，可知當y=2時，·=5(y-2)²-8有最小值-8，此時=(4,2).

    (2)當=(4,2)，即y=2時，有=(-3,5)，=(1，-1)，||=,||=,

    ·=(-3)×1+5×(-1)=-8,∴cos∠AXB===-.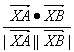

講評：向量的坐標表示與運算可以大大簡化數量積的運算，由于有關長度、角度和垂直問題可以利用向量的數量積來解決，因此，我們可以利用向量的直角坐標去研究有關長度、角度和垂直問題.