
【題目】如圖,已知四棱錐![]() ,
,![]() 是等邊三角形,
是等邊三角形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點.
的中點.
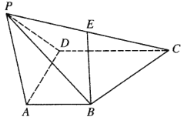
(Ⅰ)證明:直線![]() 平面
平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)證明見解析;(Ⅱ)![]()
【解析】
(Ⅰ)先證明![]() 與平面
與平面![]() 中的一條線平行,再應用線面平行的判定定理即可證得結果;
中的一條線平行,再應用線面平行的判定定理即可證得結果;
(Ⅱ)過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,過點
,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,由此可推出
,由此可推出![]() 為點
為點![]() 到平面
到平面![]() 的距離,然后通過解直角三角形求解即可.
的距離,然后通過解直角三角形求解即可.
(Ⅰ)證明:取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點,
的中點,
所以![]() 且
且![]() ,
,
又![]() 且
且![]() ,
,
所以![]() ,且
,且![]() ,
,
所以四邊形![]() 為平行四邊形,
為平行四邊形,
所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() .
.
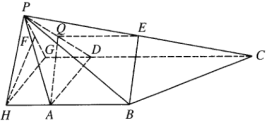
(Ⅱ)過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,過點
,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,
,
由![]() ,
,![]() ,
,![]() ,
,
得![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
過點![]() 作
作![]() 于點
于點![]() ,則
,則![]() 平面
平面![]() ,
,
由![]() 知,點
知,點![]() 到平面
到平面![]() 的距離等于
的距離等于![]() ,
,
設![]() ,則由
,則由![]() 知
知![]() ,
,![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,又
,又![]() ,
,
![]() ,則
,則![]() ,
,
![]() ,
,
即![]() ,解得
,解得![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
可得![]() ,
,
設直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,則
,則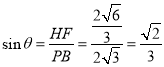 ,
,
即直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】培養某種水生植物需要定期向培養植物的水中加入物質![]() ,已知向水中每投放1個單位的物質
,已知向水中每投放1個單位的物質![]() ,
,![]() (單位:天)時刻后水中含有物質
(單位:天)時刻后水中含有物質![]() 的量增加
的量增加![]() ,
,![]() 與
與![]() 的函數關系可近似地表示為關系可近似地表示為
的函數關系可近似地表示為關系可近似地表示為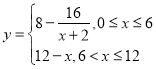 .根據經驗,當水中含有物質
.根據經驗,當水中含有物質![]() 的量不低
的量不低![]() 時,物質
時,物質![]() 才能有效發揮作用.
才能有效發揮作用.
(1)若在水中首次投放1個單位的物質![]() ,計算物質
,計算物質![]() 能持續有效發揮作用幾天?
能持續有效發揮作用幾天?
(2)若在水中首次投放1個單位的物質![]() ,第8天再投放1個單位的物質
,第8天再投放1個單位的物質![]() ,試判斷第8天至第12天,水中所含物質
,試判斷第8天至第12天,水中所含物質![]() 的量是否始終不超過
的量是否始終不超過![]() ,并說明理由.
,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為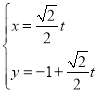 (t為參數),以原點O為極點,x正半軸為極軸建立極坐標系,曲線的極坐標方程為
(t為參數),以原點O為極點,x正半軸為極軸建立極坐標系,曲線的極坐標方程為![]() .
.
(1)求直線l的普通方程和曲線C的直角坐標方程;
(2)設P(0,-1),直線l與C的交點為M,N,線段MN的中點為Q,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
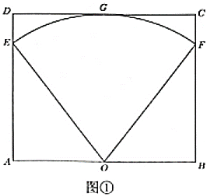
【題目】某公園計劃在矩形空地上建造一個扇形花園如圖①所示,矩形![]() 的
的![]() 邊與
邊與![]() 邊的長分別為48米與40米,扇形的圓心
邊的長分別為48米與40米,扇形的圓心![]() 為
為![]() 中點,扇形的圓弧端點
中點,扇形的圓弧端點![]() ,
,![]() 分別在
分別在![]() 與
與![]() 上,圓弧的中點
上,圓弧的中點![]() 在
在![]() 上.
上.
(1)求扇形花園的面積(精確到1平方米);
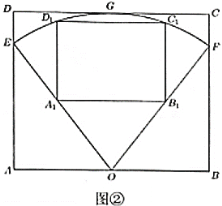
(2)若在扇形花園內開辟出一個矩形區域![]() 為花卉展覽區.如圖②所示,矩形
為花卉展覽區.如圖②所示,矩形![]() 的四條邊與矩形
的四條邊與矩形![]() 的對應邊平行,點
的對應邊平行,點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上,點
上,點![]() ,
,![]() 在扇形的弧上.某同學猜想:當矩形
在扇形的弧上.某同學猜想:當矩形![]() 面積最大時,兩矩形
面積最大時,兩矩形![]() 與
與![]() 的形狀恰好相同(即長與寬之比相同),試求花卉展覽區
的形狀恰好相同(即長與寬之比相同),試求花卉展覽區![]() 面積的最大值,并判斷上述猜想是否正確(請說明理由).
面積的最大值,并判斷上述猜想是否正確(請說明理由).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正項數列![]() 中,
中,![]() ,點
,點![]() 在拋物線
在拋物線![]() 上.數列
上.數列![]() 中,點
中,點![]() 在經過點
在經過點![]() ,以
,以![]() 為方向向量的直線
為方向向量的直線![]() 上.
上.
(1)求數列![]() ,
,![]() 的通項公式;
的通項公式;
(2)若 ,問是否存在
,問是否存在![]() ,使得
,使得![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,說明理由;
的值;若不存在,說明理由;
(3)對任意的正整數![]() ,不等式
,不等式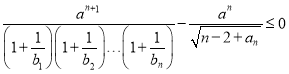 成立,求正數
成立,求正數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,有一種賽車跑道類似“梨形”曲線,由圓弧![]() 和線段AB,CD四部分組成,在極坐標系Ox中,A(2,
和線段AB,CD四部分組成,在極坐標系Ox中,A(2,![]() ),B(1,
),B(1,![]() ),C(1,
),C(1,![]() ),D(2,
),D(2,![]() ),弧
),弧![]() 所在圓的圓心分別是(0,0),(2,0),曲線M1是弧
所在圓的圓心分別是(0,0),(2,0),曲線M1是弧![]() ,曲線M2是弧
,曲線M2是弧![]() .
.
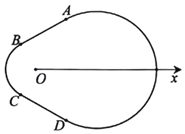
(1)分別寫出M1,M2的極坐標方程:
(2)點E,F位于曲線M2上,且![]() ,求△EOF面積的取值范圍.
,求△EOF面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四棱錐P﹣ABCD中,AB∥CD,AB⊥BC,AB=BC=1,PA=CD=2,PA⊥底面ABCD,E在PB上.
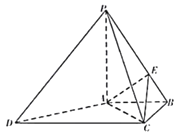
(1)證明:AC⊥PD;
(2)若PE=2BE,求三棱錐P﹣ACE的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com