
【題目】已知函數y=log2 ![]() log4
log4 ![]() +
+ ![]() (2≤x≤2m , m>1,m∈R)
(2≤x≤2m , m>1,m∈R)
(1)求x=4 ![]() 時對應的y值;
時對應的y值;
(2)求該函數的最小值.
【答案】
(1)解:x=4 ![]() 時,y=log2
時,y=log2 ![]() log4
log4 ![]() +
+ ![]() =
= ![]() =
= ![]()
(2)解:y=log2 ![]() log4
log4 ![]() +
+ ![]() =(log2x﹣3)(
=(log2x﹣3)( ![]() log2x﹣
log2x﹣ ![]() +
+ ![]() ,
,
設t=log2x,t∈[1,m],∴y= ![]() ﹣2t+2=
﹣2t+2= ![]()
1<m≤2時,函數在[1,m]上單調遞減,ymin= ![]() ﹣2m+2;
﹣2m+2;
m>2時,函數在[1,2]上單調遞減,在[2,m]上單調遞增,t=2時,ymin=0,
綜上:ymin= 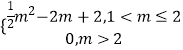
【解析】(1)代入計算,可得x=4 ![]() 時對應的y值;(2)換元,配方求該函數的最小值.
時對應的y值;(2)換元,配方求該函數的最小值.
【考點精析】解答此題的關鍵在于理解正弦函數的單調性的相關知識,掌握正弦函數的單調性:在![]()
![]() 上是增函數;在
上是增函數;在![]()
![]() 上是減函數,以及對三角函數的最值的理解,了解函數
上是減函數,以及對三角函數的最值的理解,了解函數![]() ,當
,當![]() 時,取得最小值為
時,取得最小值為![]() ;當
;當![]() 時,取得最大值為
時,取得最大值為![]() ,則
,則![]() ,
,![]() ,
,![]() .
.


 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:高中數學 來源: 題型:
【題目】太極圖是由黑白兩個魚形紋組成的圖案,俗稱陰陽魚,太極圖展現了一種相互轉化,相互統一的和諧美.定義:能夠將圓![]() 的周長和面積同時等分成兩部分的函數稱為圓
的周長和面積同時等分成兩部分的函數稱為圓![]() 的一個“太極函數”.下列有關說法中:
的一個“太極函數”.下列有關說法中:

①對圓![]() 的所有非常數函數的太極函數中,一定不能為偶函數;
的所有非常數函數的太極函數中,一定不能為偶函數;
②函數![]() 是圓
是圓![]() 的一個太極函數;
的一個太極函數;
③存在圓![]() ,使得
,使得![]() 是圓
是圓![]() 的太極函數;
的太極函數;
④直線![]() 所對應的函數一定是圓
所對應的函數一定是圓![]() 的太極函數.
的太極函數.
所有正確說法的序號是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某賽季,甲、乙兩名籃球運動員都參加了7場比賽,他們所有比賽得分的情況用如圖所示的莖葉圖表示.
(1)求甲、乙兩名運動員得分的中位數;
(2)你認為哪位運動員的成績更穩定?
(3)如果從甲、乙兩位運動員的7場得分中各隨機抽取一場的得分,求甲的得分大于乙的得分的概率.
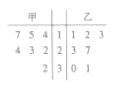
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在R上的偶函數,已知x≥0時,f(x)=x2﹣2x. 
(1)畫出偶函數f(x)的圖像的草圖,并求函數f(x)的單調遞增區間;
(2)當直線y=k(k∈R)與函數y=f(x)恰有4個交點時,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設全集U={(x,y)|x,y∈R},集合M={(x,y)| ![]() =1},N={(x,y)|y=x+1},則N∩(UM)等于( )
=1},N={(x,y)|y=x+1},則N∩(UM)等于( )
A.
B.{(2,3)}
C.(2,3)
D.{(x,y)|y=x+1}
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種商品在近30天內每件的銷售價格P(元)與時間t(天)的函數關系式近似滿足P= ![]() ,商品的日銷售量Q(件)與時間t(天)的函數關系式近似滿足Q=﹣t+40(1≤t≤30,t∈N).
,商品的日銷售量Q(件)與時間t(天)的函數關系式近似滿足Q=﹣t+40(1≤t≤30,t∈N).
(1)求這種商品日銷售金額y與時間t的函數關系式;
(2)求y的最大值,并指出日銷售金額最大的一天是30天中第幾天.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙三名學生參加某電視臺舉辦的國學知識競賽,在本次競賽中只有過關和不過關兩種結果,假設甲、乙、丙競賽過關的概率分別為![]() ,且他們競賽過關與否互不影響.
,且他們競賽過關與否互不影響.
(1)求在這次國學知識競賽中,甲、乙、丙三名學生至少有一名學生過關的概率;
(2)記在這次國學知識競賽中,甲、乙、丙三名學生過關的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望
的分布列和數學期望![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com