
分析 ①由面面平行則法向量共線,反之亦然判斷;②由面面垂直的定義判斷;③由線在垂直的性持定理判斷;④由面面垂直的定義判斷.
解答 解:①中平面α,β是指不重合兩平面,由$\overrightarrow{n_1}$∥$\overrightarrow{n_2}$⇒α∥β,由α∥β⇒$\overrightarrow{n_1}$∥$\overrightarrow{n_2}$,正確;
②α⊥β,則α與β成90°角,由圓的內接四邊形對頂角互補知法向量垂直,反之當法向量垂直,則成90°,由內接四邊形對頂角互補,知兩平面垂直.正確;
③a與α共面,則a在平面內或與平面平行,∴平面的法向量與直線a垂直,正確;
④若兩個平面的法向量不垂直,則成角不是90°,則由圓內角四邊形對頂角互補知兩平面所成的角不是90°,正確.
∴正確命題的序號實數①②③④.
故答案為:①②③④.
點評 本題主要考查用向量法來解決面面平行,面面垂直等問題,是中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①②③ | B. | ①②④ | C. | ②④ | D. | ①②③④ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 命題“如果p2+q2=2,則p+q≤2”的否命題是“如果p+q>2,則p2+q2≠2” | |
| B. | 命題p:?x∈[0,1],ex≥1,命題q:?x∈R,x2+x+1<0,則p∨q為假 | |
| C. | 若($\sqrt{x}$-$\frac{1}{2\root{3}{x}}$)n的展開式中第四項為常數項,則n=5 | |
| D. | “若am2<bm2,則a<b”的逆命題為真命題. |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若a1+a2>0,則a1+a3>0 | B. | 若a1+a3>0,則a1+a2>0 | ||
| C. | 若a1>0,則S2017>0 | D. | 若a1>0,則S2016>0 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
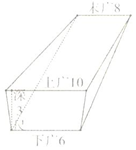 《九章算術》是東方數學思想之源,在卷五《商功》中有以下問題:今有羨除,下廣六尺,上廣一丈,深三尺,末廣八尺,無深,袤七尺,問積幾何?譯文:如圖所示的幾何體是三個側面皆為等腰梯形,其他兩面為直角三角形的五面體,(前端)下寬6尺,上寬一丈,深3尺,末端寬8尺,無深,長7尺,則它的體積是84立方尺.
《九章算術》是東方數學思想之源,在卷五《商功》中有以下問題:今有羨除,下廣六尺,上廣一丈,深三尺,末廣八尺,無深,袤七尺,問積幾何?譯文:如圖所示的幾何體是三個側面皆為等腰梯形,其他兩面為直角三角形的五面體,(前端)下寬6尺,上寬一丈,深3尺,末端寬8尺,無深,長7尺,則它的體積是84立方尺.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com