
分析 ①,y=f(x)是以π為最小正周期的周期函數;
②,∵y=f(-$\frac{π}{6}$)=0.∴f(x)的圖象關于點(-$\frac{π}{6}$,0)對稱,;
③,y=f(-$\frac{5π}{12}$)=-4為最小值∴f(x)的圖象關于直線x=-$\frac{5π}{12}$對稱;
解答 解:對于①,y=f(x)是以π為最小正周期的周期函數,故錯;
對于②,∵y=f(-$\frac{π}{6}$)=0.∴f(x)的圖象關于點(-$\frac{π}{6}$,0)對稱,故錯;
對于③,y=f(-$\frac{5π}{12}$)=-4為最小值∴f(x)的圖象關于直線x=-$\frac{5π}{12}$對稱,正確;
故答案為:③
點評 本題考查了命題真假的判定,涉及到三角函數的知識,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | $\sqrt{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
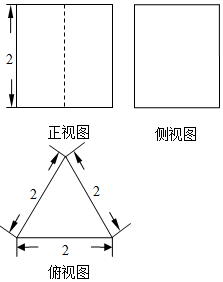 如圖所示,是一個空間幾何體的三視圖,且這個空間幾何體的所有頂點都在同一個球面上,則這個球的體積是( )
如圖所示,是一個空間幾何體的三視圖,且這個空間幾何體的所有頂點都在同一個球面上,則這個球的體積是( )| A. | $\frac{49}{9}π$ | B. | $\frac{{28\sqrt{21}}}{27}π$ | C. | $\frac{28}{3}π$ | D. | $\frac{{28\sqrt{7}}}{9}π$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 在△ABC中,若A>B,則cosA<cosB | |
| B. | 若b2=ac,則a,c的等比中項為b | |
| C. | 若命題p與p∧q為真,則q一定為真 | |
| D. | 若p:?x∈(0,+∞),lnx<x-1,則¬p:?x∈(0,+∞),lnx≥x-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
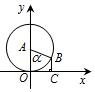 如圖,圓A的半徑為1,且A點的坐標為(0,1),B為圓上的動點,角α的始邊為射線AO,終邊為射線AB,過點B作x軸的垂線,垂足為C,將BC表示成α的函數f(α),則y=f(α)在[0,2π]的在圖象大致為( )
如圖,圓A的半徑為1,且A點的坐標為(0,1),B為圓上的動點,角α的始邊為射線AO,終邊為射線AB,過點B作x軸的垂線,垂足為C,將BC表示成α的函數f(α),則y=f(α)在[0,2π]的在圖象大致為( )| A. | 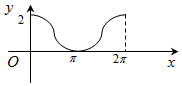 | B. | 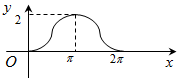 | ||
| C. | 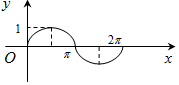 | D. | 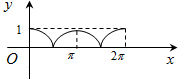 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com