
【題目】已知函數![]()
(1)若函數![]() 在定義域內單調遞增,求實數
在定義域內單調遞增,求實數 ![]() 的取值范圍,
的取值范圍,
(2)當![]() 時,關于
時,關于![]() 的方程
的方程![]() 在[1,4]上恰有兩個不相等的實數根,
在[1,4]上恰有兩個不相等的實數根,
求實數的取值范圍。
【答案】(1) (﹣∞,﹣1];(2) ln2﹣2<b≤﹣![]()
【解析】試題分析:(1)對函數f(x)進行求導,令導數大于等于0在x>0上恒成立即可.
(2)將a的值代入整理成方程的形式,然后轉化為函數考慮其圖象與x軸的交點的問題.
試題解析:
(1)f′(x)=﹣![]() ,(x>0)
,(x>0)
依題意f'(x)≥0在x>0時恒成立,即ax2+2x﹣1≤0在x>0恒成立.
則a≤![]() =(
=( ![]() ﹣1)2﹣1在x>0恒成立,
﹣1)2﹣1在x>0恒成立,
即a≤((![]() ﹣1)2﹣1)min(x>0)
﹣1)2﹣1)min(x>0)
當x=1時,(![]() ﹣1)2﹣1取最小值﹣1,
﹣1)2﹣1取最小值﹣1,
∴a的取值范圍是(﹣∞,﹣1].
(2)a=﹣![]() ,f(x)=﹣
,f(x)=﹣![]() x+b,
x+b,
∴![]() x2﹣
x2﹣![]() x+lnx﹣b=0
x+lnx﹣b=0
設g(x)=![]() x2﹣
x2﹣![]() x+lnx﹣b(x>0)則g'(x)=
x+lnx﹣b(x>0)則g'(x)=![]() ,
,
列表:
X | (0,1) | 1 | (1,2) | 2 | (2,4) |
g′(x) | + | 0 | ﹣ | 0 | + |
g(x) | ↑ | 極大值 | ↓ | 極小值 | ↑ |
∴g(x)極小值=g(2)=ln2﹣b﹣2,g(x)極大值=g(1)=﹣b﹣![]() ,
,
又g(4)=2ln2﹣b﹣2
∵方程g(x)=0在[1,4]上恰有兩個不相等的實數根.
則  ,得:ln2﹣2<b≤﹣
,得:ln2﹣2<b≤﹣![]() .
.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:高中數學 來源: 題型:
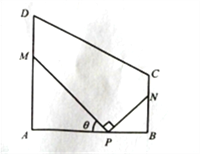
【題目】某地方政府要將一塊如圖所示的直角梯形ABCD空地改建為健身娛樂廣場.已知AD//BC, ![]() 百米,
百米, ![]() 百米,廣場入口P在AB上,且
百米,廣場入口P在AB上,且![]() ,根據規劃,過點P鋪設兩條相互垂直的筆直小路PM,PN(小路的寬度不計),點M,N分別在邊AD,BC上(包含端點),
,根據規劃,過點P鋪設兩條相互垂直的筆直小路PM,PN(小路的寬度不計),點M,N分別在邊AD,BC上(包含端點),![]() 區域擬建為跳舞健身廣場,
區域擬建為跳舞健身廣場, ![]() 區域擬建為兒童樂園,其它區域鋪設綠化草坪,設
區域擬建為兒童樂園,其它區域鋪設綠化草坪,設![]() .
.
(1)求綠化草坪面積的最大值;
(2)現擬將兩條小路PNM,PN進行不同風格的美化,PM小路的美化費用為每百米1萬元,PN小路的美化費用為每百米2萬元,試確定M,N的位置,使得小路PM,PN的美化總費用最低,并求出最小費用.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】網購已經成為一種時尚,商家為了鼓勵消費,購買時在店鋪領取優惠券,買后給予好評返還現金等促銷手段.經統計,近五年某店鋪用于促銷的費用![]() (萬元)與當年度該店鋪的銷售收人
(萬元)與當年度該店鋪的銷售收人![]() (萬元)的數據如下表:
(萬元)的數據如下表:
年份 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 |
促銷費用 |
|
|
|
|
|
銷售收入 |
|
|
|
|
|
(1)請根據上表提供的數據,用最小二乘法求出/span>![]() 關于
關于![]() 的線性回歸方
的線性回歸方![]() ;
;
(2)2018年度該店鋪預測銷售收人至少達到![]() 萬元,則該店鋪至少準備投入多少萬元的促銷費?
萬元,則該店鋪至少準備投入多少萬元的促銷費?
參考公式: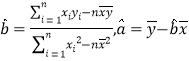
參考數據: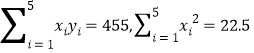
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() ,
,![]() 兩個小島相距
兩個小島相距![]() 海里,
海里,![]() 島在
島在![]() 島的正南方,現在甲船從
島的正南方,現在甲船從![]() 島出發,以
島出發,以![]() 海里/時的速度向
海里/時的速度向![]() 島行駛,而乙船同時以
島行駛,而乙船同時以![]() 海里/時的速度離開
海里/時的速度離開![]() 島向南偏東
島向南偏東![]() 方向行駛,行駛多少時間后,兩船相距最近?并求出兩船的最近距離.
方向行駛,行駛多少時間后,兩船相距最近?并求出兩船的最近距離.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求![]() 的值;
的值;
(2)若函數![]() 在區間
在區間![]() 是單調遞增函數,求實數
是單調遞增函數,求實數![]() 的取值范圍;
的取值范圍;
(3)若關于![]() 的方程
的方程![]() 在區間
在區間![]() 內有兩個實數根
內有兩個實數根![]() ,記
,記![]() ,求實數
,求實數![]() 的取值范圍 .
的取值范圍 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了解用戶對其產品的滿意度,從A,B兩地區分別隨機調查了40個用戶,根據用戶對產品的滿意度評分,得到A地區用戶滿意度評分的頻率分布直方圖和B地區用戶滿意度評分的頻數分布表。
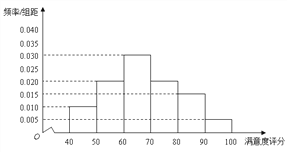
A地區用戶滿意度評分的頻率分布直方圖

B地區用戶滿意度評分的頻數分布表
(Ⅰ)在答題卡上作出B地區用戶滿意度評分的頻率分布直方圖,并通過直方圖比較兩地區滿意度評分的平均值及分散程度(不要求計算出具體值,給出結論即可);
(Ⅱ)根據用戶滿意度評分,將用戶的滿意度從低到高分為三個等級:
滿意度評分 | 低于70分 | 70分到89分 | 不低于90分 |
滿意度等級 | 不滿意 | 滿意 | 非常滿意 |
估計哪個地區的滿意度等級為不滿意的概率大?說明理由
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com