【題目】已知
為坐標原點，雙曲線
上有
兩點滿足
，且點到直線
的距離為
，則雙曲線的離心率為（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
討論直線
的斜率是否存在：當斜率不存在時，易得直線的方程，根據
及點O到直線距離即可求得
的關系，進而求得離心率；當斜率存在時，設出直線方程，聯立雙曲線方程，結合及點到直線距離即可求得離心率。
（1）當直線的斜率不存在時，由點
到直線的距離為
可知直線的方程為
所以線段
因為，根據等腰直角三角形及雙曲線對稱性可知
，即
雙曲線中滿足
所以
，化簡可得
同時除以
得
，解得
因為
，所以
（2）當直線的斜率存在時，可設直線方程為
，聯立方程可得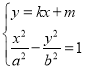
化簡可得
設
則
，
因為點到直線的距離為
則
，化簡可得
又因為
所以
化簡得
即
所以
，雙曲線中滿足
代入化簡可得
求得
，即
因為，所以
綜上所述，雙曲線的離心率為
所以選A
世紀百通期末金卷系列答案科目：高中數學 來源： 題型：
【題目】（本小題滿分12分）在一個選拔項目中，每個選手都需要進行4輪考核，每輪設有一個問題，能正確回答者進入下一輪考核，否則被淘汰。已知某選手能正確回答第一、二、三、四輪問題的概率分別為
、
、
、
，且各輪問題能否正確回答互不影響。
（Ⅰ）求該選手進入第三輪才被淘汰的概率；
（Ⅱ）求該選手至多進入第三輪考核的概率；
（Ⅲ）該選手在選拔過程中回答過的問題個數記為
，求隨機變量的分布列和期望。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（14分）已知a，b為常數，且a≠0，函數f（x）=﹣ax+b+axlnx，f（e）=2（e=2.71828…是自然對數的底數）．
（I）求實數b的值；
（II）求函數f（x）的單調區間；
（III）當a=1時，是否同時存在實數m和M（m＜M），使得對每一個t∈[m，M]，直線y=t與曲線y=f（x）（x∈[
，e]）都有公共點？若存在，求出最小的實數m和最大的實數M；若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在長方
中，
，
，E為
的中點，以
為折痕，把
折起到
的位置，且平面
平面
.
（1）求證:
；
（2）在棱
上是否存在一點P，使得
平面
，若存在，求出點P的位置，若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】《九章算術》卷五《商功》中有如下敘述“今有芻甍，下廣三丈，袤四丈，上袤二丈，無廣，高一丈“芻甍”指的是底面為矩形的對稱型屋脊狀的幾何體，“下廣三丈”是指底面矩形寬三丈，“袤四丈”是指底面矩形長四丈，“上袤二丈”是指脊長二丈，“無寬”是指脊無寬度，“高一丈”是指幾何體的高為一丈．現有一個芻甍如圖所示，下廣三丈，袤四丈，上袤三丈，無廣，高二丈，則該芻甍的外接球的表面積為_______________平方丈．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
