
 函數f(x)是R上的奇函數,且當x>0時,函數的解析式為f(x)=log2(x+1).
函數f(x)是R上的奇函數,且當x>0時,函數的解析式為f(x)=log2(x+1).分析 (1)當x<0時,-x>0,結合函數f(x)是R上的奇函數,且當x>0時,函數的解析式為f(x)=log2(x+1),可得答案;
(2)根據f(0)=0及(1)中結論,可得分段函數形式的函數f(x)的解析式,進而得到函數的圖象.
解答 解:(1)當x<0時,-x>0,
此時f(-x)=log2(-x+1).
又由函數f(x)是R上的奇函數,
故f(x)=-f(-x)=-log2(-x+1).
(2)又∵定義在R上的奇函數f(x)滿足f(0)=0,
故f(x)=$\left\{\begin{array}{l}-{log}_{2}(-x+1),x<0\\ 0,x=0\\{log}_{2}(x+1),x>0\end{array}\right.$,
函數的圖象如下圖所示: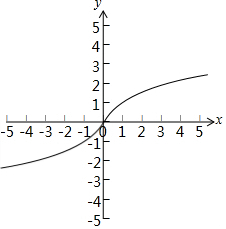
點評 本題考查的知識點是函數的奇偶性,函數解析式的求法,函數的圖象,難度中檔.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中數學 來源: 題型:解答題
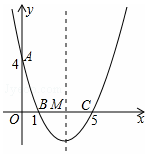 如圖,在平面直角坐標系中,拋物線經過點A(0,4),B(1,0),C(5,0),其對稱軸與x 軸相交于點M.
如圖,在平面直角坐標系中,拋物線經過點A(0,4),B(1,0),C(5,0),其對稱軸與x 軸相交于點M.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{6}$,$\frac{1}{6}$ | B. | $\frac{1}{2}$,$\frac{2}{3}$ | C. | $\frac{1}{6}$,$\frac{2}{3}$ | D. | $\frac{2}{3}$,$\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ?a∈R,函數f(x)和g(x)都是奇函數 | B. | ?a∈R,函數f(x)和g(x)都是奇函數 | ||
| C. | ?a∈R,函數f(x)和g(x)都是偶函數 | D. | ?a∈R,函數f(x)和g(x)都是偶函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 醫生人數 | 0 | 1 | 2 | 3 | 4 | 5人以上 |
| 概率 | 0.1 | 0.16 | 0.2 | x | 0.2 | 0.04 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-5)∪(5,+∞) | B. | (-5,-2)∪(2,5) | C. | (-∞,-5)∪(-2,0) | D. | (-∞,-5)∪(-2,0)∪(2,5) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①③ | B. | ②③ | C. | ①④ | D. | ②④ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {m|m>$\frac{9}{4}$} | B. | {m|m≥$\frac{9}{4}$} | C. | {m|m<$\frac{9}{4}$} | D. | {m|m≤$\frac{9}{4}$} |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com