【題目】已知函數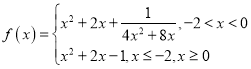
，若函數
有6個零點，則實數
的取值范圍是_________.
【答案】
【解析】
由題意首先研究函數
的性質，然后結合函數的性質數形結合得到關于a的不等式，求解不等式即可確定實數a的取值范圍.
當
時，函數
在區間
上單調遞增，
很明顯
，且存在唯一的實數
滿足
，
當
時，由對勾函數的性質可知函數
在區間
上單調遞減，在區間
上單調遞增，
結合復合函數的單調性可知函數
在區間
上單調遞減，在區間
上單調遞增，且當
時，
，
考查函數
在區間
上的性質，
由二次函數的性質可知函數在區間
上單調遞減，在區間
上單調遞增，
函數
有6個零點，即方程
有6個根，
也就是
有6個根，即
與
有6個不同交點，
注意到函數
關于直線
對稱，則函數關于直線對稱，
繪制函數的圖像如圖所示，
觀察可得：
，即
.
綜上可得，實數
的取值范圍是.
故答案為．
奪冠訓練單元期末沖刺100分系列答案
新思維小冠軍100分作業本系列答案
名師指導一卷通系列答案科目：高中數學 來源： 題型：
【題目】某研究機構為了解某學校學生使用手機的情況，在該校隨機抽取了60名學生（其中男、女生人數之比為2：1）進行問卷調查.進行統計后將這60名學生按男、女分為兩組，再將每組學生每天使用手機的時間（單位：分鐘）分為
5組，得到如圖所示的頻率分布直方圖（所抽取的學生每天使用手機的時間均不超過50分鐘）.
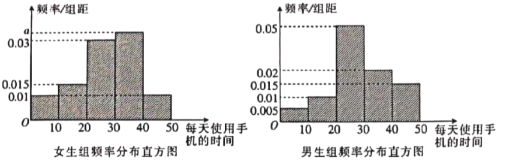
（1）求出女生組頻率分布直方圖中
的值；
（2）求抽取的60名學生中每天使用手機時間不少于30分鐘的學生人數.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列
，
及函數
（
），
（
）．
（1）若等比數列滿足
，
，
，求數列
的前
（）項和；
（2）已知等差數列滿足
，
，
（
、
均為常數，
，且
），
（）．試求實數對(，)，使得
成等比數列．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數
（其中
）.
（1）判斷函數
的奇偶性，并說明理由；
（2）求函數的反函數
（3）若兩個函數
與
在區間
上恒滿足
，則函數與在閉區間上是分離的．試判斷的反函數
與
在閉區間
上是否分離？若分離，求出實數
的取值范圍；若不分離，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}滿足：a1+a2+a3+…+an=n-an，（n=1，2，3，…）
（Ⅰ）求證：數列{an-1}是等比數列；
（Ⅱ）令bn=（2-n）（an-1）（n=1，2，3，…），如果對任意n∈N*，都有bn+
t≤t2，求實數t的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】中國歷法推測遵循以測為輔、以算為主的原則.例如《周髀算經》和《易經》里對二十四節氣的晷（guǐ）影長的記錄中，冬至和夏至的晷影長是實測得到的，其它節氣的晷影長則是按照等差數列的規律計算得出的.下表為《周髀算經》對二十四節氣晷影長的記錄，其中
寸表示115寸
分（1寸=10分）.
節氣 | 冬至 | 小寒 （大雪） | 大寒 （小雪） | 立春 （立冬） | 雨水 （霜降） | 驚蟄 （寒露） | 春分 （秋分） | 清明 （白露） | 谷雨 （處暑） | 立夏 （立秋） | 小滿 （大暑） | 芒種 （小暑） | 夏至 |
晷影長 （寸 | 135 |
|
|
|
|
| 75.5 |
|
|
|
|
| 16.0 |
已知《易經》中記錄某年的冬至晷影長為130.0寸，夏至晷影長為14.8寸，按照上述規律那么《易經》中所記錄的春分的晷影長應為( )
A.91.6寸B.82.0寸C.81.4寸D.72.4寸
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
