【題目】如圖，設
是棱長為
的正方體的一個頂點，過從此頂點出發的三條棱的中點作截面，對正方體的所有頂點都如此操作，所得的各截面與正方體各面共同圍成一個多面體，則關于此多面體有以下結論：①有
個頂點；②有
條棱；③有個面；④表面積為
；⑤體積為
．其中正確的結論是____________．（要求填上所有正確結論的序號）
【答案】①②⑤
【解析】
解：如圖，
原來的六個面還在只不過是變成了一個小正方形，再添了八個頂點各對應的一個三角形的面，所以總計6+8=14個面，故③錯；
每個正方形4條邊，每個三角形3條邊，4×6+3×8=48，考慮到每條邊對應兩個面，所以實際只有
×48=24條棱．②正確；
所有的頂點都出現在原來正方體的棱的中點位置，
原來的棱的數目是12，所以現在的頂點的數目是12．
或者從圖片上可以看出每個頂點對應4條棱，每條棱很明顯對應兩個頂點，所以頂點數是棱數的一半即12個．①正確；
三角形和四邊形的邊長都是
a，所以正方形總面積為6××a2=3a2，三角形總面積為8××a2sin60°=
a2，表面積（3+）a2，故④錯；
體積為原正方形體積減去8個三棱錐體積，每個三棱錐體積為8×
（
）3=a2，剩余總體積為a3-a3=
a3⑤正確．
故答案為：①②⑤．
同步練習強化拓展系列答案科目：高中數學 來源： 題型：
【題目】某地的出租車價格規定：起步費
元，可行
公里，公里以后按每公里
元計算，可再行
公里；超過
公里按每公里
元計算，假設不考慮堵車和紅綠燈等所引起的費用，也不考慮實際收取費用去掉不足一元的零頭等實際情況，即每一次乘車的車費由行車里程唯一確定。
（1）若小明乘出租車從學校到家，共
公里，請問他應付出租車費多少元？
（2）求車費
（元）與行車里程
（公里）之間的函數關系式
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】學校藝術節對同一類的
，
，
，
四項參賽作品，只評一項一等獎，在評獎揭曉前，甲、乙、丙、丁四位同學對這四項參賽作品預測如下：
甲說：“是或作品獲得一等獎”；
乙說：“作品獲得一等獎”；
丙說：“，兩項作品未獲得一等獎”；
丁說：“是作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的，則獲得一等獎的作品是__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，底面為矩形的四棱錐
，
底面
，
，
，
是
的中點.
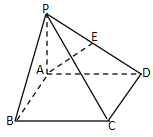
（1）求四棱錐的體積；
（2）求
與面所成角；
（3）在
邊上是否存在一點
，使得
到平面
的距離為
？若存在，求出；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示：在五面體ABCDEF中，四邊形EDCF是正方形，AD＝DE＝1，∠ADE＝90°，∠ADC＝∠DCB＝120°．
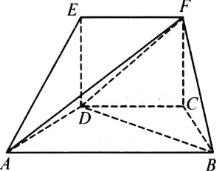
（Ⅰ）求證：平面ABCD⊥平面EDCF；
（Ⅱ）求三棱錐A－BDF的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖是某地區2012年至2018年生活垃圾無害化處理量（單位：萬噸）的折線圖.
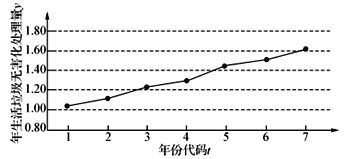
注：年份代碼
分別表示對應年份
.
（1）由折線圖看出，可用線性回歸模型擬合
與
的關系，請用相關系數
（
線性相關較強）加以說明；
（2）建立與的回歸方程(系數精確到0.01)，預測2019年該區生活垃圾無害化處理量.
（參考數據）
，
，
，
，
，
，
.
（參考公式）相關系數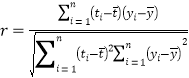
，在回歸方程
中斜率和截距的最小二乘估計公式分別為：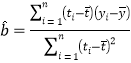
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，
，
， O為DE的中點，
．F為
的中點，平面
平面BCED．
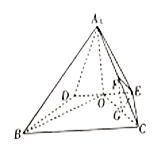
（1）求證：平面 
平面
．
（2）線段OC上是否存在點G，使得
平面EFG？說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
