
已知橢圓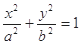 (
(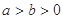 )右頂點到右焦點的距離為
)右頂點到右焦點的距離為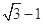 ,短軸長為
,短軸長為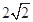 .
.
(Ⅰ)求橢圓的方程;
(Ⅱ)過左焦點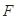 的直線與橢圓分別交于
的直線與橢圓分別交于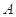 、
、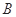 兩點,若線段
兩點,若線段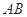 的長為
的長為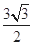 ,求直線
,求直線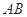 的方程.
的方程.
(Ⅰ)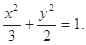 ;(Ⅱ)
;(Ⅱ)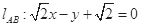 或
或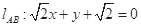 .
.
【解析】
試題分析:(Ⅰ)由題意列關于a、b、c的方程組,解方程得a、b、c的值,既得橢圓的方程;(Ⅱ)分兩種情況討論:當直線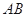 與
與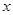 軸垂直時,
軸垂直時,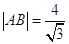 ,此時
,此時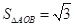 不符合題意故舍掉;當直線
不符合題意故舍掉;當直線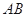 與
與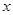 軸不垂直時,設直線
軸不垂直時,設直線 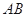 的方程為:
的方程為: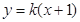 ,代入橢圓方程消去
,代入橢圓方程消去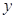 得:
得: ,再由韋達定理得
,再由韋達定理得 ,從而可得直線的方程.
,從而可得直線的方程.
試題解析:(Ⅰ)由題意,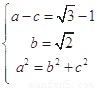 ,解得
,解得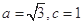 ,即:橢圓方程為
,即:橢圓方程為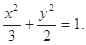 4分
4分
(Ⅱ)當直線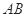 與
與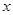 軸垂直時,
軸垂直時,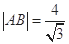 ,此時
,此時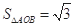 不符合題意故舍掉;
6分
不符合題意故舍掉;
6分
當直線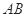 與
與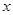 軸不垂直時,設直線
軸不垂直時,設直線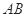 的方程為:
的方程為: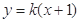 ,
,
代入消去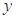 得:
得: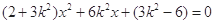 .
.
設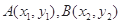 ,則
,則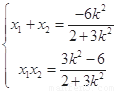 8分
8分
所以 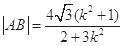 ,
11分
,
11分
由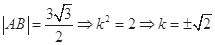 , 13分
, 13分
所以直線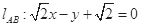 或
或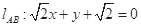 .
14分
.
14分
考點:1、橢圓的方程;2、直線被圓錐曲線所截弦長的求法;3、韋達定理.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
 如圖所示,F1,F2分別為橢圓C:
如圖所示,F1,F2分別為橢圓C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
查看答案和解析>>
科目:高中數學 來源:2011年浙江省杭州市高二寒假作業數學理卷二 題型:解答題
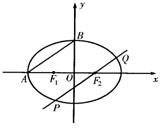
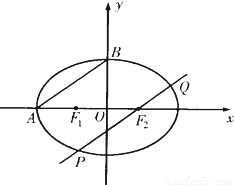
如圖所示,F1、F2分別為橢圓C: 的左、右兩個焦點,A、B為兩個頂點,
的左、右兩個焦點,A、B為兩個頂點,
已知橢圓C上的點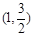 到F1、F2兩點的距離之和為4.
到F1、F2兩點的距離之和為4.
(Ⅰ)求橢圓C的方程和焦點坐標;
(Ⅱ)過橢圓C的焦點F2作AB的平行線交橢圓于P、Q兩點,求△F1PQ的面積.
查看答案和解析>>
科目:高中數學 來源:安徽省期末題 題型:解答題
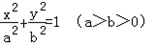 的左、右兩個焦點,A、B為兩個頂點,已知橢圓C上的點
的左、右兩個焦點,A、B為兩個頂點,已知橢圓C上的點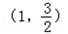 到F1、F2兩點的距離之和為4.
到F1、F2兩點的距離之和為4.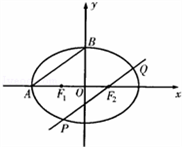
查看答案和解析>>
科目:高中數學 來源:2008-2009學年浙江省杭州高級中學高二(上)期末數學試卷(文科)(解析版) 題型:解答題
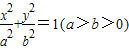 的左、右兩個焦點,A,B為兩個頂點,已知橢圓C上的點到F1,F2兩點的距離之和為4且
的左、右兩個焦點,A,B為兩個頂點,已知橢圓C上的點到F1,F2兩點的距離之和為4且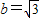 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com