
分析 利用復合函數的性質判斷函數的單調性,求出f(x)的最值,根據零點個數得出最值與0的關系,從而可求得m的范圍.
解答 解:y=$\left\{\begin{array}{l}{(\frac{1}{2})^{1-x}+m,x≤1}\\{(\frac{1}{2})^{x-1}+m,m>1}\end{array}\right.$,
∴函數y=($\frac{1}{2}$)|1-x|+m在(-∞,1]上單調遞增,在(1,+∞)上單調遞減,
∴當x=1時,y取得最大值m+1,
∵($\frac{1}{2}$)|1-x|>0,
∴m<f(x)≤m+1.
∵函數有兩個零點,
∴$\left\{\begin{array}{l}{m<0}\\{m+1>0}\end{array}\right.$,解得:-1<m<0.
故答案為:(-1,0).
點評 本題考查了函數的零點與單調性的關系,函數單調性的判斷,屬于中檔題.


 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
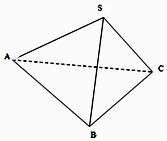 如圖,已知三棱錐S-ABC中,SA=SB=CA=CB=$\sqrt{3}$,AB=2,SC=$\sqrt{2}$,則二面角S-AB-C的平面角的大小為( )
如圖,已知三棱錐S-ABC中,SA=SB=CA=CB=$\sqrt{3}$,AB=2,SC=$\sqrt{2}$,則二面角S-AB-C的平面角的大小為( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在四棱錐P-ABCD中,O為AC與BD的交點,AB⊥平面PAD,△PAD是正三角形,DC∥AB,DA=DC=2AB=2a.
如圖,在四棱錐P-ABCD中,O為AC與BD的交點,AB⊥平面PAD,△PAD是正三角形,DC∥AB,DA=DC=2AB=2a.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | lnx0 | B. | $ln\sqrt{x_0}$ | C. | ln(lnx0) | D. | ${(ln{x_0})^2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {(x-1)(x+2)=0} | B. | {y|y=x+1,x∈Z} | C. | {x|(x+1)(x-2)=0} | D. | {x|(x-1)(x+2)=0} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5}{4}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com