
【題目】已知橢圓C:![]() +
+![]() =1(a>b>0)的兩個焦點分別為F1(﹣2,0),F2(2,0),離心率為
=1(a>b>0)的兩個焦點分別為F1(﹣2,0),F2(2,0),離心率為![]() .過焦點F2的直線l(斜率不為0)與橢圓C交于A,B兩點,線段AB的中點為D,O為坐標原點,直線OD交橢圓于M,N兩點.
.過焦點F2的直線l(斜率不為0)與橢圓C交于A,B兩點,線段AB的中點為D,O為坐標原點,直線OD交橢圓于M,N兩點.
(Ⅰ)求橢圓C的方程;
(Ⅱ)當四邊形MF1NF2為矩形時,求直線l的方程.
【答案】(Ⅰ)![]() ;(Ⅱ)y=
;(Ⅱ)y=![]() .
.
【解析】
試題(I)由已知可得: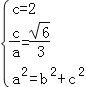 ,解得即可得出;
,解得即可得出;
(II)由題意可知直線l的斜率存在,設直線l方程為y=k(x﹣2),A(x1,y1),B(x2,y2),M(x3,y3),N(﹣x3,﹣y3).與橢圓方程聯立化為(1+3k2)x2﹣12k2x+12k2﹣6=0,.利用根與系數的關系、中點坐標公式可得:線段AB的中點D![]() ,可得直線OD的方程為:x+3ky=0(k≠0).與橢圓方程聯立,解得
,可得直線OD的方程為:x+3ky=0(k≠0).與橢圓方程聯立,解得![]() =
=![]() ,x3=﹣3ky3.利用四邊形MF1NF2為矩形,可得
,x3=﹣3ky3.利用四邊形MF1NF2為矩形,可得![]() =0,解出即可.
=0,解出即可.
解:(I)由已知可得: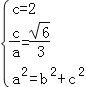 ,
,
解得a2=6,b2=2,
∴橢圓C的方程為![]() ;
;
(II)由題意可知直線l的斜率存在,
設直線l方程為y=k(x﹣2),A(x1,y1),B(x2,y2),M(x3,y3),N(﹣x3,﹣y3).
聯立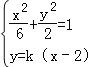 ,化為(1+3k2)x2﹣12k2x+12k2﹣6=0,
,化為(1+3k2)x2﹣12k2x+12k2﹣6=0,
∴x1+x2=![]() ,y1+y2=k(x1+x2﹣4)=
,y1+y2=k(x1+x2﹣4)=![]() ,
,
∴線段AB的中點D![]() ,
,
∴直線OD的方程為:x+3ky=0(k≠0).
聯立![]() ,解得
,解得![]() =
=![]() ,x3=﹣3ky3.
,x3=﹣3ky3.
∵四邊形MF1NF2為矩形,
∴![]() =0,
=0,
∴(x3﹣2,y3)(﹣x3﹣2,﹣y3)=0,
∴![]() =0,
=0,
∴![]() =0,解得k=
=0,解得k=![]() ,
,
故直線方程為y=![]() .
.


 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案科目:高中數學 來源: 題型:
【題目】已知曲線C的參數方程為![]() (t為參數),以原點O為極點,x軸的非負半軸為極軸建立極坐標系,過極點的兩射線
(t為參數),以原點O為極點,x軸的非負半軸為極軸建立極坐標系,過極點的兩射線![]() 、
、![]() 相互垂直,與曲線C分別相交于A、B兩點(不同于點O),且
相互垂直,與曲線C分別相交于A、B兩點(不同于點O),且![]() 的傾斜角為銳角
的傾斜角為銳角![]() .
.
(1)求曲線C和射線![]() 的極坐標方程;
的極坐標方程;
(2)求△OAB的面積的最小值,并求此時![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型娛樂場有兩種型號的水上摩托,管理人員為了了解水上摩托的使用情況及給娛樂城帶來的經濟收入情況,對該場所最近6年水上摩托的使用情況進行了統計,得到相關數據如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代碼x | 1 | 2 | 3 | 4 | 5 | 6 |
使用率 | 11 | 13 | 16 | 15 | 20 | 21 |
(Ⅰ)請根據以上數據,用最小二乘法求水上摩托使用率![]() 關于年份代碼
關于年份代碼![]() 的線性回歸方程,并預測該娛樂場2019年水上摩托的使用率;
的線性回歸方程,并預測該娛樂場2019年水上摩托的使用率;
(Ⅱ)隨著生活水平的提高,外出旅游的老百姓越來越多,該娛樂場根據自身發展需求,準備重新進購一批水上摩托,其型號主要是目前使用的Ⅰ型、Ⅱ型兩種,每輛價格分別為1萬元、![]() 萬元.根據以往經驗,每輛水上摩托的的使用年限不超過四年.娛樂場管理部對已經淘汰的兩款水上摩托的使用情況分別抽取了50輛進行統計,使用年限如條形圖所示:
萬元.根據以往經驗,每輛水上摩托的的使用年限不超過四年.娛樂場管理部對已經淘汰的兩款水上摩托的使用情況分別抽取了50輛進行統計,使用年限如條形圖所示:
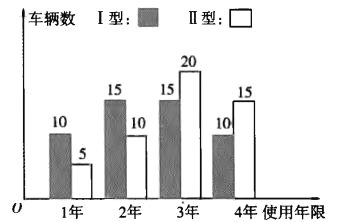
已知每輛水上摩托從購入到淘汰平均年收益是![]() 萬元,若用頻率作為概率,以每輛水上摩托純利潤(純利潤=收益-購買成本)的期望值為參考值,則該娛樂場的負責人應選哪種型號的水上摩托?
萬元,若用頻率作為概率,以每輛水上摩托純利潤(純利潤=收益-購買成本)的期望值為參考值,則該娛樂場的負責人應選哪種型號的水上摩托?
附:線性回歸方程為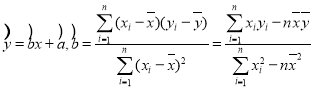 ,
,![]() ,
,
參考數據:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“總把新桃換舊符”(王安石)、“燈前小草寫桃符”(陸游),春節是中華民族的傳統節日,在宋代人們用寫“桃符”的方式來祈福避禍,而現代人們通過貼“福”字、貼春聯、掛燈籠等方式來表達對新年的美好祝愿,某商家在春節前開展商品促銷活動,顧客凡購物金額滿50元,則可以從“福”字、春聯和燈籠這三類禮品中任意免費領取一件,若有4名顧客都領取一件禮品,則他們中有且僅有2人領取的禮品種類相同的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知向量
中,已知向量![]() ,
,![]() ,且
,且![]() .記動點
.記動點![]() 的軌跡為
的軌跡為![]() .
.
(1)求![]() 的方程;
的方程;
(2)已知直線![]() 過坐標原點,且與(1)中的軌跡
過坐標原點,且與(1)中的軌跡![]() 交于
交于![]() 兩點,
兩點,![]() 在第三象限,且
在第三象限,且![]() 軸,垂足為
軸,垂足為![]() ,連接
,連接![]() 并延長交
并延長交![]() 于點
于點![]() ,求
,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
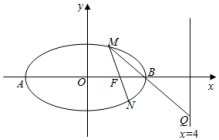
【題目】在平面直角坐標系xOy中,橢圓C的中心在坐標原點O,其右焦點為![]() ,且點
,且點![]() 在橢圓C上.
在橢圓C上.
![]() 求橢圓C的方程;
求橢圓C的方程;
![]() 設橢圓的左、右頂點分別為A、B,M是橢圓上異于A,B的任意一點,直線MF交橢圓C于另一點N,直線MB交直線
設橢圓的左、右頂點分別為A、B,M是橢圓上異于A,B的任意一點,直線MF交橢圓C于另一點N,直線MB交直線![]() 于Q點,求證:A,N,Q三點在同一條直線上.
于Q點,求證:A,N,Q三點在同一條直線上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市氣象部門根據2018年各月的每天最高氣溫平均數據,繪制如下折線圖,那么,下列敘述錯誤的是( )
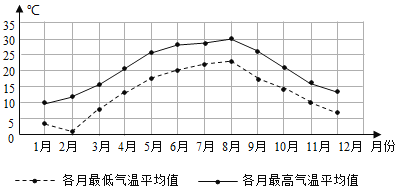
A.各月最高氣溫平均值與最低氣溫平均值總體呈正相關
B.全年中,2月份的最高氣溫平均值與最低氣溫平均值的差值最大
C.全年中各月最低氣溫平均值不高于10°C的月份有5個
D.從2018年7月至12月該市每天最高氣溫平均值與最低氣溫平均值呈下降趨勢
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com