
分析 (1)求出函數的導數,計算f(1),f′(1),求出切線方程即可;
(2)求出函數的導數,通過討論a的范圍求出函數的單調區間即可;
(3)設F(x)=ex-x-1,求出函數的導數,問題轉化為x>0時,ex+$\frac{e}{3}$x3-1>x,設h(x)=xex-ex-$\frac{e}{3}$x3+1,根據函數的單調性確定a的范圍即可.
解答 解:(1)a=e時,f(x)=ex-ex-1,f(1)=-1,
f′(x)=ex-e,可得f′(1)=0,
故a=e時,函數f(x)在切點(1,f(1))處的切線方程是y=-1;
(2)f(x)=ex-ax-1,f′(x)=ex-a,
當a≤0時,f′(x)>0,則f(x)在R上單調遞增;
當a>0時,令f′(x)=ex-a=0,得x=lna,
∵f(x)的定義域為(0,+∞).
則f(x)在(0,lna]上單調遞減,在(lna,+∞)上單調遞增.
(3)設F(x)=ex-x-1,則F′(x)=ex-1,
∵x=0時,F′(x)=0,x>0時,F′(x)>0,
∴F(x)在[0,+∞)遞增,
∴x>0時,F(x)>F(0),化簡得:ex-1>x,
∴x>0時,ex+$\frac{e}{3}$x3-1>x,
設h(x)=xex-ex-$\frac{e}{3}$x3+1,
則h′(x)=x(ex-ex),
設H(x)=ex-ex,H′(x)=ex-e,
由H′(x)=0,得x=1時,H′(x)>0,
x<1時,H′(x)<0,
∴x>0時,H(x)的最小值是H(1),
x>0時,H(x)≥H(1),即H(x)≥0,
∴h′(x)≥0,可知函數h(x)在(0,+∞)遞增,
∴h(x)>h(0)=0,化簡得ex+$\frac{e}{3}$x3-1<xex,
∴x>0時,x<ex+$\frac{e}{3}$x3-1<xex,
∴x>0時,lnx<ln(ex+$\frac{e}{3}$x3-1)<lnx+x,
即0<ln(ex+$\frac{e}{3}$x3-1)-lnx<x,
即x>0時,0<g(x)<x,
當a≤1時,由(2)得f(x)在(0,+∞)遞增,
得f(g(x))<f(x)滿足條件,
當a>1時,由(2)得f(x)在(0,lna)遞減,
∴0<x≤lna時,f(g(x))>f(x),與已知?x>0,f(g(x))<f(x)矛盾,
綜上,a的范圍是(-∞,1].
點評 本題考查了切線方程問題,考查函數的單調性、最值問題,考查導數的應用以及分類討論思想、轉化思想,是一道綜合題.


 巧學巧練系列答案
巧學巧練系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
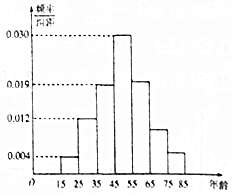 2016年雙十一活動結束后,某地區研究人員為了研究該地區在雙十一活動中消費超過3000元的人群的年齡狀況,隨機在當地消費超過3000元的群眾中抽取了500人作調查,所得頻率分布直方圖如圖所示:
2016年雙十一活動結束后,某地區研究人員為了研究該地區在雙十一活動中消費超過3000元的人群的年齡狀況,隨機在當地消費超過3000元的群眾中抽取了500人作調查,所得頻率分布直方圖如圖所示:查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com