
分析 首先建立平面直角坐標系:以A為原點,平行于CB的直線為x軸,這樣便可建立坐標系,然后便可根據條件確定出C,B點的坐標,并根據題意設P(cosθ,sinθ),從而得到$\overrightarrow{BQ}$的坐標,用θ表示|$\overrightarrow{BQ}$|即可.
解答 解:如圖建立平面直角坐標系,設P(cosθ,sinθ),則A(0,0),B(-$\frac{3}{2}$,-$\frac{3\sqrt{3}}{2}$),C($\frac{3}{2}$,-$\frac{3\sqrt{3}}{2}$);
$\overrightarrow{AQ}$=$\frac{2}{3}$$\overrightarrow{AP}$+$\frac{1}{3}$$\overrightarrow{AC}$=$\frac{2}{3}(cosθ,sinθ)+\frac{1}{3}(\frac{3}{2},-\frac{3\sqrt{3}}{2})$=($\frac{2}{3}cosθ+\frac{1}{2},\frac{2}{3}sinθ-\frac{\sqrt{3}}{2}$).
$\overrightarrow{BQ}=\overrightarrow{BA}+\overrightarrow{AQ}$=($\frac{2}{3}cosθ+2,\frac{2}{3}sinθ+\sqrt{3}$)
則|$\overrightarrow{BQ}$|=$\sqrt{(\frac{2}{3}cosθ+2)^{2}+(\frac{2}{3}sinθ+\sqrt{3})^{2}}$=$\sqrt{\frac{67}{9}+\frac{4\sqrt{7}}{3}sin(θ+α)}≥\sqrt{\frac{67}{9}-\frac{4\sqrt{7}}{3}}$=$\sqrt{\frac{67-12\sqrt{7}}{9}}=\frac{3\sqrt{7}-2}{3}$.
∴故答案為:$\frac{3\sqrt{7}-2}{3}$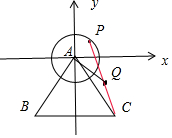
點評 本題考查了數量積運算性質、三角函數的性質,考查了推理能力與計算能力,屬于中檔題


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
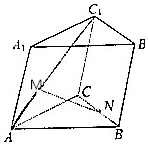 如圖所示,已知斜三棱柱ABC-A1B1C1,點M,N分別在AC1和BC上,且滿足$\overrightarrow{AM}$=k$\overrightarrow{A{C}_{1}}$,$\overrightarrow{BN}$=k$\overrightarrow{BC}$(0≤k≤1).
如圖所示,已知斜三棱柱ABC-A1B1C1,點M,N分別在AC1和BC上,且滿足$\overrightarrow{AM}$=k$\overrightarrow{A{C}_{1}}$,$\overrightarrow{BN}$=k$\overrightarrow{BC}$(0≤k≤1).查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
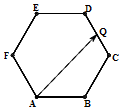
| A. | $\overrightarrow{AB}•\overrightarrow{AQ}$ | B. | $\overrightarrow{AC}•\overrightarrow{AQ}$ | C. | $\overrightarrow{AD}•\overrightarrow{AQ}$ | D. | $\overrightarrow{AE}•\overrightarrow{AQ}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
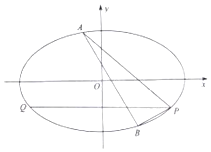 已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{3}}{2}$,并且過點P(2,-1)
已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{3}}{2}$,并且過點P(2,-1)查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{6}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com