
分析 根據題意,有函數的奇偶性可得f(-$\frac{9}{2}$)=-f($\frac{9}{2}$),結合f(x+2)=f(x),分析可得函數f(x)的周期T=2,進而可得f($\frac{9}{2}$)=f($\frac{9}{2}$-2×2)=f($\frac{1}{2}$),結合函數的解析式可得f($\frac{1}{2}$)的值,又由于f(-$\frac{9}{2}$)=-f($\frac{9}{2}$),即可得答案.
解答 解:根據題意,函數f(x)為奇函數,則有f(-$\frac{9}{2}$)=-f($\frac{9}{2}$),
又由函數f(x)滿足f(x+2)=f(x),
函數f(x)的周期T=2,
則f($\frac{9}{2}$)=f($\frac{9}{2}$-2×2)=f($\frac{1}{2}$),
又由當0≤x≤1時,f(x)=2x(1-x),
則f($\frac{1}{2}$)=2×$\frac{1}{2}$×(1-$\frac{1}{2}$)=$\frac{1}{2}$,
故f(-$\frac{9}{2}$)=-f($\frac{9}{2}$)=-$\frac{1}{2}$;
故答案為:-$\frac{1}{2}$.
點評 本題考查函數的奇偶性與周期性,關鍵是利用函數的奇偶性與周期性,分析得到f(-$\frac{9}{2}$)與f($\frac{1}{2}$)的關系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{9}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{π}{4}$ | B. | -$\frac{3π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | 02 | B. | 13 | C. | 42 | D. | 44 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-3,1] | B. | (-∞,1] | C. | [1,3) | D. | (3,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
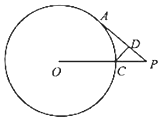 如圖,過圓O外一點P作圓O的切線PA,切點為A,連接OP與圓O交于點C,過點C作圓O作AP的垂線,垂足為D,若PA=2$\sqrt{5}$,PC:PO=1:3,求CD的長.
如圖,過圓O外一點P作圓O的切線PA,切點為A,連接OP與圓O交于點C,過點C作圓O作AP的垂線,垂足為D,若PA=2$\sqrt{5}$,PC:PO=1:3,求CD的長.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com