
【題目】已知二次函數(shù)![]() 在
在![]() 處取得極值,且在
處取得極值,且在![]() 點(diǎn)處的切線與直線
點(diǎn)處的切線與直線![]() 平行.
平行.
(1)求![]() 的解析式;
的解析式;
(2)求函數(shù)![]() 的單調(diào)遞增區(qū)間及極值。
的單調(diào)遞增區(qū)間及極值。
(3)求函數(shù)![]() 在
在![]() 的最值。
的最值。
【答案】(1)![]() .
.
(2)增區(qū)間為![]() ,
,![]() .在
.在![]() 有極小值為0。在
有極小值為0。在![]() 有極大值4/27。
有極大值4/27。
(3)![]() 的最大值為2,最小值為0。
的最大值為2,最小值為0。
【解析】試題分析:(1)第一步,求函數(shù)的導(dǎo)數(shù),第二步:根據(jù)![]() 處取得極值,知
處取得極值,知![]() ,根據(jù)導(dǎo)數(shù)的幾何意義知;在
,根據(jù)導(dǎo)數(shù)的幾何意義知;在![]() 處的導(dǎo)數(shù)等于
處的導(dǎo)數(shù)等于![]() ,解得
,解得![]() ,第三步,代入寫出
,第三步,代入寫出![]() ,令
,令![]() ,得到極值點(diǎn),最后,解出
,得到極值點(diǎn),最后,解出![]() ;(2)根據(jù)(1)得到的結(jié)論,可知
;(2)根據(jù)(1)得到的結(jié)論,可知![]() 上的單調(diào)性,以及極值,比較端點(diǎn)值和極值的大小,就得到最大值和最小值.
上的單調(diào)性,以及極值,比較端點(diǎn)值和極值的大小,就得到最大值和最小值.
試題解析:解:(1) 由![]() ,可得
,可得![]() .由題設(shè)可得
.由題設(shè)可得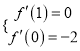
即![]() .解得
.解得![]() ,
, ![]() .所以
.所以![]() .
.
由題意得![]()
所以![]() .
.
令![]() ,得
,得![]() ,
, ![]() .
.
當(dāng)![]() 變化時,
變化時, ![]() ,
, ![]() 變化情況如下表:
變化情況如下表:
|
|
|
|
|
|
|
|
|
|
|
|
| 單調(diào)遞增 | 4/27 | 單調(diào)遞減 | 0 | 單調(diào)遞增 |
所以函數(shù)![]() 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為![]() ,
,![]() .
.
(2)因?yàn)樵?/span>![]() 時函數(shù)
時函數(shù)![]() 有極小值為0.在
有極小值為0.在![]() 時函數(shù)
時函數(shù)![]() 有極大值
有極大值![]() .
.
又![]() ,
,
所以函數(shù)![]() 的最大值為2,最小值為0.
的最大值為2,最小值為0.


 小天才課時作業(yè)系列答案
小天才課時作業(yè)系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗(yàn)系列答案
黃岡小狀元滿分沖刺微測驗(yàn)系列答案 新輔教導(dǎo)學(xué)系列答案
新輔教導(dǎo)學(xué)系列答案 陽光同學(xué)一線名師全優(yōu)好卷系列答案
陽光同學(xué)一線名師全優(yōu)好卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若函數(shù)![]() 上是減函數(shù),求實(shí)數(shù)a的最小值;
上是減函數(shù),求實(shí)數(shù)a的最小值;
(Ⅲ)若![]() ,
,![]() ,使
,使![]() 成立,求實(shí)數(shù)a的取值范圍.
成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的右焦點(diǎn)為
的右焦點(diǎn)為![]() ,且點(diǎn)
,且點(diǎn)![]() 在橢圓
在橢圓![]() 上.
上.
⑴求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
⑵已知動直線![]() 過點(diǎn)
過點(diǎn)![]() 且與橢圓
且與橢圓![]() 交于
交于![]() 兩點(diǎn).試問
兩點(diǎn).試問![]() 軸上是否存在定點(diǎn)
軸上是否存在定點(diǎn)![]() ,使得
,使得![]() 恒成立?若存在,求出點(diǎn)Q的坐標(biāo);若不存在,請說明理由.
恒成立?若存在,求出點(diǎn)Q的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(2)若關(guān)于![]() 的不等式
的不等式![]() 恒成立,求整數(shù)
恒成立,求整數(shù)![]() 的最小值;
的最小值;
(3)若正實(shí)數(shù)![]() 滿足
滿足![]() ,證明:
,證明: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如下五個命題:
①在線性回歸模型中, ![]() 表示解釋變量對于預(yù)報變量變化的貢獻(xiàn)率,在對女大學(xué)生的身高預(yù)報體重的回歸分析數(shù)據(jù)中,算得
表示解釋變量對于預(yù)報變量變化的貢獻(xiàn)率,在對女大學(xué)生的身高預(yù)報體重的回歸分析數(shù)據(jù)中,算得![]() ,表明“女大學(xué)生的體重差異有64%是由身高引起的”
,表明“女大學(xué)生的體重差異有64%是由身高引起的”
②隨機(jī)變量的方差和標(biāo)準(zhǔn)差都反映了隨機(jī)變量取值偏離于均值的平均程度,方差或標(biāo)準(zhǔn)差越小,則隨機(jī)變量偏離于均值的平均程度越大;
③正態(tài)曲線關(guān)于直線![]() 對稱,這個曲線只有當(dāng)
對稱,這個曲線只有當(dāng)![]() 時,才在
時,才在![]() 軸上方;
軸上方;
④正態(tài)曲線的對稱軸由![]() 確定,當(dāng)
確定,當(dāng)![]() 一定時,曲線的形狀由
一定時,曲線的形狀由![]() 決定,并且
決定,并且![]() 越大,曲線越“矮胖”;
越大,曲線越“矮胖”;
⑤若隨機(jī)變量![]() ,且
,且![]() 則
則![]() ;
;
其中正確命題的序號是
A. ②③ B. ①④⑤ C. ①④ D. ①③④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的方程為
的方程為![]() ,雙曲線
,雙曲線![]() 的一條漸近線與
的一條漸近線與![]() 軸所成的夾角為
軸所成的夾角為![]() ,且雙曲線的焦距為
,且雙曲線的焦距為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)![]() 分別為橢圓
分別為橢圓![]() 的左,右焦點(diǎn),過
的左,右焦點(diǎn),過![]() 作直線
作直線![]() (與
(與![]() 軸不重合)交橢圓于
軸不重合)交橢圓于![]() ,
, ![]() 兩點(diǎn),線段
兩點(diǎn),線段![]() 的中點(diǎn)為
的中點(diǎn)為![]() ,記直線
,記直線![]() 的斜率為
的斜率為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(數(shù)學(xué)文卷·2017屆湖北省黃岡市高三上學(xué)期期末考試第16題) “中國剩余定理”又稱“孫子定理”.1852年英國來華傳教偉烈亞利將《孫子算經(jīng)》中“物不知數(shù)”問題的解法傳至歐洲.1874年,英國數(shù)學(xué)家馬西森指出此法符合1801年由高斯得出的關(guān)于同余式解法的一般性定理,因而西方稱之為“中國剩余定理”. “中國剩余定理”講的是一個關(guān)于整除的問題,現(xiàn)有這樣一個整除問題:將2至2017這2016個數(shù)中能被3除余1且被5除余1的數(shù)按由小到大的順序排成一列,構(gòu)成數(shù)列![]() ,則此數(shù)列的項(xiàng)數(shù)為__________.
,則此數(shù)列的項(xiàng)數(shù)為__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的焦距為
)的焦距為![]() ,且經(jīng)過點(diǎn)
,且經(jīng)過點(diǎn)![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)![]() 、
、![]() 是橢圓
是橢圓![]() 上兩點(diǎn),線段
上兩點(diǎn),線段![]() 的垂直平分線
的垂直平分線![]() 經(jīng)過
經(jīng)過![]() ,求
,求![]() 面積的最大值(
面積的最大值(![]() 為坐標(biāo)原點(diǎn)).
為坐標(biāo)原點(diǎn)).
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com