
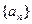 ,
,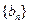 滿足
滿足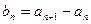 ,其中
,其中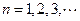 .
.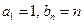 ,求數列
,求數列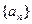 的通項公式;
的通項公式;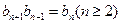 ,且
,且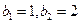 .
.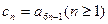 ,求證:數列
,求證:數列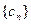 為等差數列;
為等差數列;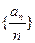 中任意一項的值均未在該數列中重復出現無數次. 求首項
中任意一項的值均未在該數列中重復出現無數次. 求首項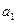 應滿足的條件.
應滿足的條件.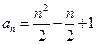

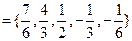 ,
,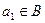 時,數列
時,數列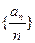 中必有某數重復出現無數次.
中必有某數重復出現無數次.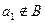 時,
時,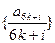
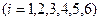 均為單調數列,任意一個數在這6個數列中最多出現一次,所以數列
均為單調數列,任意一個數在這6個數列中最多出現一次,所以數列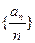 中任意一項的值均未在該數列中重復出現無數次
中任意一項的值均未在該數列中重復出現無數次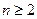 時,有
時,有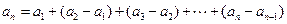
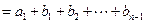 …………2分
…………2分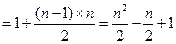 . ………………3分
. ………………3分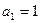 也滿足上式,所以數列
也滿足上式,所以數列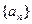 的通項為
的通項為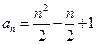 .…………4分
.…………4分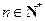 有
有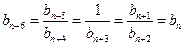 ,………………5分
,………………5分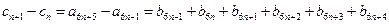
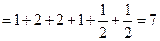
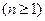 ,
,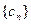 為等差數列. ………………7分
為等差數列. ………………7分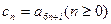 ,(其中
,(其中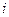 為常數且
為常數且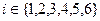 ),所以
),所以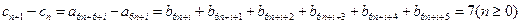
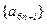 均為以7為公差的等差數列. ………………9分
均為以7為公差的等差數列. ………………9分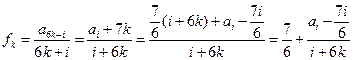 ,
,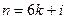
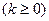 ,
,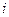 為
為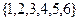 中的一個常數),
中的一個常數),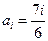 時,對任意的
時,對任意的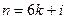 有
有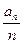
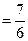 ; ………………10分
; ………………10分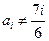 時,
時,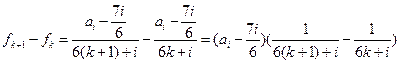
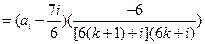 ……………11分
……………11分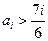 ,則對任意的
,則對任意的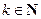 有
有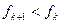 ,所以數列
,所以數列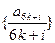 為單調減數列;
為單調減數列;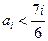 ,則對任意的
,則對任意的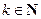 有
有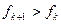 ,所以數列
,所以數列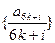 為單調增數列;…12分
為單調增數列;…12分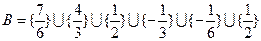
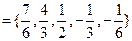 ,
,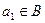 時,數列
時,數列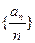 中必有某數重復出現無數次.
中必有某數重復出現無數次.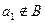 時,
時,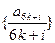
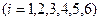 均為單調數列,任意一個數在這6個數列中最多出現一次,所以數列
均為單調數列,任意一個數在這6個數列中最多出現一次,所以數列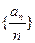 中任意一項的值均未在該數列中重復出現無數次. ……14分
中任意一項的值均未在該數列中重復出現無數次. ……14分

 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:高中數學 來源:不詳 題型:解答題
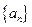 的前
的前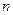 項和為
項和為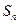 ,滿足
,滿足
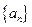 的通項公式;
的通項公式; 滿足
滿足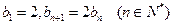 ,
,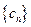 滿足
滿足 ,數列
,數列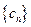 的前
的前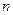
 項和為
項和為 ,求
,求 ;
; ,甲同學利用第(2)問中的
,甲同學利用第(2)問中的 ,試圖確定
,試圖確定 的值是否可以等于2011?為此,他設計了一個程序
的值是否可以等于2011?為此,他設計了一個程序 (如圖),但乙同學認為這個程序如果被執行會是一個“死循環”(即程序會永遠循環下去,而無法結束),你是否同意乙同學的觀點?請說明理由。
(如圖),但乙同學認為這個程序如果被執行會是一個“死循環”(即程序會永遠循環下去,而無法結束),你是否同意乙同學的觀點?請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com