
【題目】設函數f(x)= ![]() x3+ax2﹣8x﹣1(a<0).若曲線y=f(x)的切線斜率的最小值是﹣9.求:
x3+ax2﹣8x﹣1(a<0).若曲線y=f(x)的切線斜率的最小值是﹣9.求:
(1)a的值;
(2)函數f(x)的極值.
【答案】
(1)解:∵f(x)= ![]() x3+ax2﹣8x﹣1,
x3+ax2﹣8x﹣1,
∴f′(x)=x2+2ax﹣8.
∴當x=﹣a時,f′(x)有最小值﹣a2﹣8
由已知:﹣a2﹣8=﹣9,∴a2=1
∵a<0,∴a=﹣1
(2)解:由(1)f′(x)=x2﹣2x﹣8
令f′(x)=0得x=﹣2或4
當x變化時,f′(x)及f(x)的變化情況如下表:
x | (﹣∞,﹣2) | ﹣2 | (﹣2,4) | 4 | (4,+∞) |
f′(x) | + | 0 | ﹣ | 0 | + |
f(x) | 極大值 | 極小值 |
∴當x=﹣2時,f(x)取得極大值,極大值為f(﹣2)= ![]() ;
;
當x=4時,f(x)取得極小值,極小值為f(4)=﹣ ![]()
【解析】(1)先求出導函數的最小值,利用曲線y=f(x)的切線斜率的最小值是﹣9,求出a的值即可;(2)先求導數fˊ(x),在函數的定義域內解不等式fˊ(x)>0和fˊ(x)<0,確定函數的單調區間可得函數f(x)的極大值和極小值.
【考點精析】解答此題的關鍵在于理解函數的極值與導數的相關知識,掌握求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值.
是極小值.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:高中數學 來源: 題型:
【題目】在棱長為2的正方體ABCD﹣A1B1C1D1中,E,F分別為A1B1 , CD的中點. 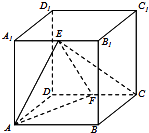
(1)求| ![]() |
|
(2)求直線EC與AF所成角的余弦值;
(3)求二面角E﹣AF﹣B的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本題滿分12分)已知函數f(x)=2cos x(sin x+cos x).
(1)求f![]() 的值;
的值;
(2)求函數f(x)的最小正周期及單調遞增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知下列四個命題:
p1:若直線l和平面α內的無數條直線垂直,則l⊥α;
p2:若f(x)=2x﹣2﹣x , 則x∈R,f(﹣x)=﹣f(x);
p3:若 ![]() ,則x0∈(0,+∞),f(x0)=1;
,則x0∈(0,+∞),f(x0)=1;
p4:在△ABC中,若A>B,則sinA>sinB.
其中真命題的個數是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】二次函數f(x)的圖象經過點(0, ![]() ),且f′(x)=﹣x﹣1,則不等式f(10x)>0的解集為( )
),且f′(x)=﹣x﹣1,則不等式f(10x)>0的解集為( )
A.(﹣3,1)
B.(﹣lg3,0)
C.( ![]() ,1)
,1)
D.(﹣∞,0)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 某廠生產不同規格的一種產品,根據檢測標準,其合格產品的質量![]() 與尺寸
與尺寸![]() 之間近似滿足關系式
之間近似滿足關系式![]() (
(![]() 為大于
為大于![]() 的常數),現隨機抽取
的常數),現隨機抽取![]() 件合格產品,測得數據如下:
件合格產品,測得數據如下:
尺寸 |
|
|
|
|
|
|
質量 |
|
|
|
|
|
|
對數據作了初步處理,相關統計量的值如下表:
|
|
|
|
|
|
|
|
(1)根據所給數據,求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(2)按照某項指標測定,當產品質量與尺寸的比在區間![]() 內時為優等品,現從抽取的
內時為優等品,現從抽取的![]() 件合格產品中再任選
件合格產品中再任選![]() 件,記
件,記![]() 為取到優等品的件數,試求隨機變量
為取到優等品的件數,試求隨機變量![]() 的分布列和期望.
的分布列和期望.
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
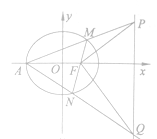
【題目】已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,
, ![]() 為該橢圓的右焦點,過點
為該橢圓的右焦點,過點![]() 任作一直線
任作一直線![]() 交橢圓于
交橢圓于![]() 兩點,且
兩點,且![]() 的最大值為4.
的最大值為4.
(1)求橢圓![]() 的方程;
的方程;
(2)設橢圓![]() 的左頂點為
的左頂點為![]() ,若直線
,若直線![]() 分別交直線
分別交直線![]() 于
于![]() 兩點,求證:
兩點,求證: ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com