
分析 (1)根據奇偶性的定義直接判斷即可.
(2)分離參數法,轉化成二次函數問題求解.
解答 解:(1)函數f(x)=2x+$\frac{a}{2^x}$-1(a為實數).
當a=1時,f(x)=2x+2-x-1,
∵f(-x)=2-x+2x-1=f(x),
∴y=f(x)為偶函數.
(2)由題意:函數f(x)=2x+$\frac{a}{2^x}$-1(a為實數).
任意x∈R時f(x)≥0,即2x+$\frac{a}{2x}$-1≥0
?a≥2x-(2x)2,
令t=2x>0,則:a≥-t2+t(t>0).
對任意x∈R時f(x)≥0恒成立,只要當t>0時,a≥(-t2+t)max.
根據二次函數的圖象及性質:
可得:當t=$\frac{1}{2}$時,可得(-t2+t)max=$\frac{1}{4}$,
∴a≥$\frac{1}{4}$.
故得a的取值范圍是[$\frac{1}{4}$,+∞).
點評 本題考查了函數的奇偶性的判斷和分離參數法轉化為二次函數問題解決恒成立問題.屬于中檔題.


科目:高中數學 來源: 題型:填空題
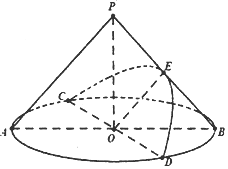 如圖,在底面半徑和高均為4的圓錐中,AB、CD是底面圓O的兩條互相垂直的直徑,E是母線PB的中點,若過直徑CD與點E的平面與圓錐側面的交線是以E為頂點的拋物線的一部分,則該拋物線的焦點到圓錐頂點P的距離為$\sqrt{10}$.
如圖,在底面半徑和高均為4的圓錐中,AB、CD是底面圓O的兩條互相垂直的直徑,E是母線PB的中點,若過直徑CD與點E的平面與圓錐側面的交線是以E為頂點的拋物線的一部分,則該拋物線的焦點到圓錐頂點P的距離為$\sqrt{10}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 某人在草地上散步,看到他西方有兩根相距6米的標桿A、B,當他向正北方向步行3分鐘后,看到標桿B在其西南方向上,根標桿A在其南偏西30°方向上,求此人步行的速度.(要求用鉛筆畫出圖形,標出字母與相關數據)
某人在草地上散步,看到他西方有兩根相距6米的標桿A、B,當他向正北方向步行3分鐘后,看到標桿B在其西南方向上,根標桿A在其南偏西30°方向上,求此人步行的速度.(要求用鉛筆畫出圖形,標出字母與相關數據)查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com