
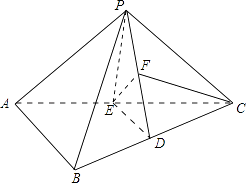
【題目】如圖,三棱錐P﹣ABC中,D,E分別是BC,AC的中點.PB=PC=AB=2,AC=4,BC=2 ![]() ,PA=
,PA= ![]() .
. 
(1)求證:平面ABC⊥平面PED;
(2)求AC與平面PBC所成的角;
(3)求平面PED與平面PAB所成銳二面角的余弦值.
【答案】
(1)證明:∵PB=PC=AB=2,AC=4,BC=2 ![]() ,PA=
,PA= ![]() ,
,
∴AB2+BC2=AC2;
∴BC⊥AB;
D,E分別是BC,AC中點;
∴DE∥AB;
∴BC⊥DE;
又PB=PC,D是BC中點;
∴BC⊥PD,DE∩PD=D;
∴BC⊥平面PED
(2)證明:解: PA= ![]() ,PC=2,AC=4,
,PC=2,AC=4,
∴由余弦定理cos∠PCA= ![]() ,
,
在△PCE中,PC=2,CE=2,
∴由余弦定理得PE=1,DE=1,∴PD=1;
∴△PDE為等邊三角形;
∴如圖,取PD中點F,連接EF,CF,則:EF⊥PD;
又BC⊥平面PED,EF平面PED;
∴BC⊥EF,即EF⊥BC,PD∩BC=D;
∴EF⊥平面PBC;
∴∠ECF是直線AC和平面PBC所成角;
EF= ![]() ,CE=2;
,CE=2;
∴sin∠ECF= ![]() =
= ![]() =
= ![]() ,
,
∴直線AC與平面PBC所成角為arcsin ![]()
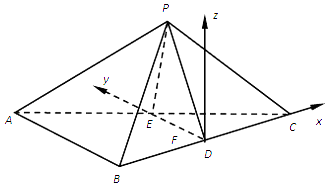
(3)證明:以D為原點,分別以DC,DE為x,y軸,建立如圖所示的空間直角坐標系,
B(﹣ ![]() ,0,0),C(
,0,0),C( ![]() ,0,0),E(0,1,0),A(﹣
,0,0),E(0,1,0),A(﹣ ![]() ,2,0),
,2,0),
設P(0,y,z),則由PC=2,PA= ![]() ,
,
得 ![]() ,解得y=
,解得y= ![]() ,z=
,z= ![]() ,∴P(0,
,∴P(0, ![]() ),
),
設平面PAB的法向量 ![]() =(x1,y1,z1),
=(x1,y1,z1),
∵ ![]() =(0,2,0),
=(0,2,0), ![]() =(
=( ![]() ),
),
∴  ,取x11,得
,取x11,得 ![]() =(1,0,﹣2),
=(1,0,﹣2),
平面PED的法向量為 ![]() =(1,0,0),
=(1,0,0),
∴cos< ![]() >
>
= ![]() ,
,
∴平面PED與平面PAB所成銳二面角的余弦值為 ![]()
【解析】(1)根據AB,BC,AC邊的長度容易得到BC⊥AB,E,D都是中點,從而DE∥AB,這便得到BC⊥DE,而由PB=PC,D為BC邊中點,從而便得到BC⊥PD,從而由線面垂直的判定定理即得BC⊥平面PED;(2)取PD中點F,連接EF,CF,則∠ECF是直線AC和平面PBC所成角,由此能求出直線AC與平面PBC所成角.(3)以D為原點,分別以DC,DE為x,y軸,建立空間直角坐標系,利用向量法能求出平面PED與平面PAB所成銳二面角的余弦值.
【考點精析】利用平面與平面垂直的判定和空間角的異面直線所成的角對題目進行判斷即可得到答案,需要熟知一個平面過另一個平面的垂線,則這兩個平面垂直;已知![]() 為兩異面直線,A,C與B,D分別是
為兩異面直線,A,C與B,D分別是![]() 上的任意兩點,
上的任意兩點,![]() 所成的角為
所成的角為![]() ,則
,則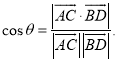 .
.


科目:高中數學 來源: 題型:
【題目】如圖,位于A處的信息中心獲悉:在其正東方向相距40海里的B處有一艘漁船遇險,在原地等待營救.信息中心立即把消息告知在其南偏西30°、相距20海里的C處的乙船,現乙船朝北偏東θ的方向即沿直線CB前往B處救援,則cosθ=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將A,B兩枚骰子各拋擲一次,觀察向上的點數,問:
(1)共有多少種不同的結果?
(2)兩枚骰子點數之和是3的倍數的結果有多少種?
(3)兩枚骰子點數之和是3的倍數的概率為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD中,AB⊥AC,AB⊥PA,AB∥CD,E,F,G,M,N分別為PB,AB,BC,PD,PC的中點.求證:平面EFG⊥平面EMN.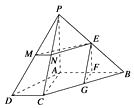
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列結論中,正確的是( )
A.冪函數的圖象都通過點(0,0),(1,1)
B.冪函數的圖象可以出現在第四象限
C.當冪指數α取1,3, ![]() 時,冪函數y=xα是增函數
時,冪函數y=xα是增函數
D.當冪指數α=-1時,冪函數y=xα在定義域上是減函數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,且 ![]() bcosA=asinB.
bcosA=asinB.
(1)求角A的大小;
(2)若a=6,△ABC的面積是9 ![]() ,求三角形邊b,c的長.
,求三角形邊b,c的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐D﹣ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E為BC點,F棱AC上,且AF=3FC. 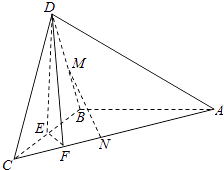
(1)求三棱錐D﹣ABC的體積;
(2)求證:AC⊥平面DEF;
(3)若M為DB中點,N在棱AC上,且CN= ![]() CA,求證:MN∥平面DEF.
CA,求證:MN∥平面DEF.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AF=BF,EC∥FD,FD⊥底面ABCD,M是AB的中點. 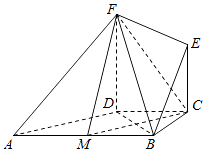
(1)求證:平面CFM⊥平面BDF;
(2)點N在CE上,EC=2,FD=3,當CN為何值時,MN∥平面BEF.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com