
【題目】已知二次函數![]()
(1)若函數在區間![]() 上存在零點,求實數
上存在零點,求實數![]() 的取值范圍;
的取值范圍;
(2)是否存在常數![]() ,當
,當![]() 時,
時,![]() 的值域為區間
的值域為區間![]() ,且區間
,且區間![]() 的長度為
的長度為![]() (視區間
(視區間![]() 的長度為
的長度為![]() ),如果存在,求出
),如果存在,求出![]() 的值;如果不存在,說明理由.
的值;如果不存在,說明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某班主任對全班50名學生進行了作業量多少的調查,喜歡玩電腦游戲的同學認為作業多的有18人,認為作業不多的有9人,不喜歡玩電腦游戲的同學認為作業多的有8人,認為作業不多的有15人,則認為喜歡玩電腦游戲與認為作業量的多少有關系的把握大約是多少?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() ,
,![]() 滿足下列條件:①
滿足下列條件:①![]() ,
,![]() ;②當
;②當![]() 時,
時,![]() 滿足:
滿足:![]() 時,
時,![]() ,
,![]() ;
;![]() 時,
時,![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 和
和![]() 的值,并猜想數列
的值,并猜想數列![]() 可能的通項公式(不需證明);
可能的通項公式(不需證明);
(2)若![]() ,
,![]() ,
,![]() 是滿足
是滿足![]() 的最大整數,求
的最大整數,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位為促進職工業務技能提升,對該單位120名職工進行一次業務技能測試,測試項目共5項.現從中隨機抽取了10名職工的測試結果,將它們編號后得到它們的統計結果如下表(表1)所示(“√”表示測試合格,“×”表示測試不合格).
表1:
編號\測試項目 | 1 | 2 | 3 | 4 | 5 |
1 | × | √ | √ | √ | √ |
2 | √ | √ | √ | √ | × |
3 | √ | √ | √ | √ | × |
4 | √ | √ | √ | × | × |
5 | √ | √ | √ | √ | √ |
6 | √ | × | × | √ | × |
7 | × | √ | √ | √ | × |
8 | √ | × | × | × | × |
9 | √ | √ | × | × | × |
10 | √ | √ | √ | √ | × |
規定:每項測試合格得5分,不合格得0分.
(1)以抽取的這10名職工合格項的項數的頻率代替每名職工合格項的項數的概率.
①設抽取的這10名職工中,每名職工測試合格的項數為![]() ,根據上面的測試結果統計表,列出
,根據上面的測試結果統計表,列出![]() 的分布列,并估計這120名職工的平均得分;
的分布列,并估計這120名職工的平均得分;
②假設各名職工的各項測試結果相互獨立,某科室有5名職工,求這5名職工中至少有4人得分不少于20分的概率;
(2)已知在測試中,測試難度的計算公式為![]() ,其中
,其中![]() 為第
為第![]() 項測試難度,
項測試難度,![]() 為第
為第![]() 項合格的人數,
項合格的人數,![]() 為參加測試的總人數.已知抽取的這10名職工每項測試合格人數及相應的實測難度如下表(表2):
為參加測試的總人數.已知抽取的這10名職工每項測試合格人數及相應的實測難度如下表(表2):
表2:
測試項目 | 1 | 2 | 3 | 4 | 5 |
實測合格人數 | 8 | 8 | 7 | 7 | 2 |
定義統計量![]() ,其中
,其中![]() 為第
為第![]() 項的實測難度,
項的實測難度,![]() 為第
為第![]() 項的預測難度(
項的預測難度(![]() ).規定:若
).規定:若![]() ,則稱該次測試的難度預測合理,否則為不合理,測試前,預估了每個預測項目的難度,如下表(表3)所示:
,則稱該次測試的難度預測合理,否則為不合理,測試前,預估了每個預測項目的難度,如下表(表3)所示:
表3:
測試項目 | 1 | 2 | 3 | 4 | 5 |
預測前預估難度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
判斷本次測試的難度預估是否合理.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對任意實數![]() ,給出下列命題:①“
,給出下列命題:①“![]() ”是“
”是“![]() ”的充要條件;②“
”的充要條件;②“![]() 是無理數”是“
是無理數”是“![]() 是無理數”的充要條件;③“
是無理數”的充要條件;③“![]() ”是“
”是“![]() ”的充分條件;④“
”的充分條件;④“![]() ”是“
”是“![]() ”的必要條件;其中真命題的個數是( )
”的必要條件;其中真命題的個數是( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中錯誤的是( )
A. 先把高二年級的2000名學生編號為1到2000,再從編號為1到50的50名學生中隨機抽取1名學生,其編號為![]() ,然后抽取編號為
,然后抽取編號為![]() ,
,![]() ,
,![]() 的學生,這樣的抽樣方法是系統抽樣法;
的學生,這樣的抽樣方法是系統抽樣法;
B. 獨立性檢驗中,![]() 越大,則越有把握說兩個變量有關;
越大,則越有把握說兩個變量有關;
C. 若兩個隨機變量的線性相關性越強,則相關系數![]() 的值越接近于1;
的值越接近于1;
D. 若一組數據1、a、3的平均數是2,則該組數據的方差是![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個命題:
①函數![]() 是奇函數且在定義域上是單調遞增函數;
是奇函數且在定義域上是單調遞增函數;
②函數![]() 有兩個零點,則
有兩個零點,則![]() ;
;
③函數![]() ,則
,則![]() 的解集為
的解集為![]() ;
;
④函數![]() 的單調遞減區間為
的單調遞減區間為![]() .
.
其中正確命題的序號為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠今年1月、2月、3月生產某產品分別為1萬件、1.2萬件、1.3萬件,為了估計以后每月的產量,以這三個月的產量為依據,用一個函數模擬該產品的月產量,![]() 與月份
與月份![]() 的關系,模擬函數可以選用二次函數或函數
的關系,模擬函數可以選用二次函數或函數![]() 、
、![]() 、
、![]() 為常數)已知四月份該產品的產量為1.37萬件,請問用以上哪個函數作模擬函數較好?說明理由.
為常數)已知四月份該產品的產量為1.37萬件,請問用以上哪個函數作模擬函數較好?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
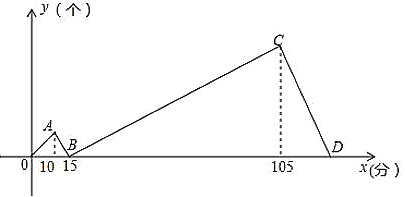
【題目】甲乙兩人同時各接受了600個零件的加工任務,甲比乙每分鐘加工的數量多,兩人同時開始加工,加工過程中甲因故障停止一會后又繼續按原速加工,直到他們完成任務.如圖表示甲比乙多加工的零件數量y(個)與加工時間x(分)之間的函數關系,A點橫坐標為10,B點坐標為![]() ,C點橫坐標為105.則甲每分鐘加工的數量是_______,點D的坐標是_______.
,C點橫坐標為105.則甲每分鐘加工的數量是_______,點D的坐標是_______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com