
【題目】已知拋物線![]() 的焦點到直線
的焦點到直線![]() 的距離為
的距離為![]() .
.
(1)求拋物線![]() 的方程;
的方程;
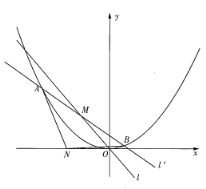
(2)如圖,若![]() ,直線
,直線![]() 與拋物線
與拋物線![]() 相交于
相交于![]() 兩點,與直線
兩點,與直線![]() 相交于點
相交于點![]() ,且
,且![]() ,求
,求![]() 面積的取值范圍.
面積的取值范圍.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】春秋以前中國已有“抱甕而出灌”的原始提灌方式,使用提水吊桿——桔槔,后發展成轆轤.19世紀末,由于電動機的發明,離心泵得到了廣泛應用,為發展機械提水灌溉提供了條件.圖形如圖所示為灌溉抽水管道在等高圖的上垂直投影,在A處測得B處的仰角為37度,在A處測得C處的仰角為45度,在B處測得C處的仰角為53度,A點所在等高線值為20米,若BC管道長為50米,則B點所在等高線值為( )(參考數據![]() )
)
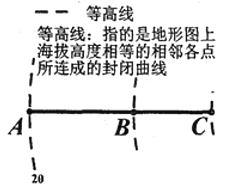
A.30米B.50米C.60米D.70米
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第二屆中國國際進口博覽會于2019年11月5日至10日在上海國家會展中心舉行.它是中國政府堅定支持貿易自由化和經濟全球化,主動向世界開放市場的重要舉措,有利于促進世界各國加強經貿交流合作,促進全球貿易和世界經濟增長,推動開放世界經濟發展.某機構為了解人們對“進博會”的關注度是否與性別有關,隨機抽取了100名不同性別的人員(男、女各50名)進行問卷調查,并得到如下![]() 列聯表:
列聯表:
男性 | 女性 | 合計 | |
關注度極高 | 35 | 14 | 49 |
關注度一般 | 15 | 36 | 51 |
合計 | 50 | 50 | 100 |
(1)根據列聯表,能否有99.9%的把握認為對“進博會”的關注度與性別有關;
(2)若從關注度極高的被調查者中按男女分層抽樣的方法抽取7人了解他們從事的職業情況,再從7人中任意選取2人談談關注“進博會”的原因,求這2人中至少有一名女性的概率.
附:![]() .
.
參考數據:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市數學教研室對全市2018級15000名的高中生的學業水平考試的數學成績進行調研,隨機選取了200名高中生的學業水平考試的數學成績作為樣本進行分析,將結果列成頻率分布表如下:
數學成績 | 頻數 | 頻率 |
| 5 | 0.025 |
| 15 | 0.075 |
| 50 | 0.25 |
| 70 | 0.35 |
| 45 | 0.225 |
| 15 | 0.075 |
合計 | 200 | 1 |
根據學業水平考試的數學成績將成績分為“優秀”、“合格”、“不合格”三個等級,其中成績大于或等于80分的為“優秀”,成績小于60分的為“不合格”,其余的成績為“合格”.
(1)根據頻率分布表中的數據,估計全市學業水平考試的數學成績的眾數、中位數(精確到0.1);
(2)市數學教研員從樣本中又隨機選取了![]() 名高中生的學業水平考試的數學成績,如果這
名高中生的學業水平考試的數學成績,如果這![]() 的最小值;
的最小值;
(3)估計全市2018級高中生學業水平考試“不合格”的人數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在極坐系中,點![]() 繞極點
繞極點![]() 順時針旋轉角
順時針旋轉角![]() 得到點
得到點![]() .以
.以![]() 為原點,極軸為
為原點,極軸為![]() 軸非負半軸,并取相同的單位長度建立平面直角坐標系,曲線
軸非負半軸,并取相同的單位長度建立平面直角坐標系,曲線![]() :
:![]() 繞
繞![]() 逆時針旋轉
逆時針旋轉![]() 得到曲線
得到曲線![]() .
.
(1)求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 過點
過點![]() 且與曲線
且與曲線![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】雙紐線最早于1694年被瑞士數學家雅各布·伯努利用來描述他所發現的曲線.在平面直角坐標系![]() 中,把到定點
中,把到定點![]() ,
,![]() 距離之積等于
距離之積等于![]() (
(![]() )的點的軌跡稱為雙紐線C.已知點
)的點的軌跡稱為雙紐線C.已知點![]() 是雙紐線C上一點,下列說法中正確的有( )
是雙紐線C上一點,下列說法中正確的有( )
①雙紐線C關于原點O中心對稱; ②![]() ;
;
③雙紐線C上滿足![]() 的點P有兩個; ④
的點P有兩個; ④![]() 的最大值為
的最大值為![]() .
.
A.①②B.①②④C.②③④D.①③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為原點,極軸為
,以極點為原點,極軸為![]() 軸非負半軸建立平面直角坐標系,直線
軸非負半軸建立平面直角坐標系,直線![]() 的參數方程為
的參數方程為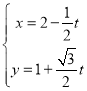 (
(![]() 為參數).
為參數).
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)在(1)中,設曲線![]() 經過伸縮變換
經過伸縮變換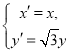 得到曲線
得到曲線![]() ,設曲線
,設曲線![]() 上任意一點為
上任意一點為![]() ,當點
,當點![]() 到直線
到直線![]() 的距離取最大值時,求此時點
的距離取最大值時,求此時點![]() 的直角坐標.
的直角坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
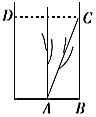
【題目】《九章算術》是我國古代內容極為豐富的數學名著,書中有一個“引葭赴岸”問題:“今有池方一丈,葭生其中央.出水一尺,引葭赴岸,適與岸齊.問水深、葭長各幾何?”其意思為“今有水池1丈見方(即![]() 尺),蘆葦生長在水的中央,長出水面的部分為1尺.將蘆葦向池岸牽引,恰巧與水岸齊接(如圖所示).試問水深、蘆葦的長度各是多少?假設
尺),蘆葦生長在水的中央,長出水面的部分為1尺.將蘆葦向池岸牽引,恰巧與水岸齊接(如圖所示).試問水深、蘆葦的長度各是多少?假設![]() ,現有下述四個結論:
,現有下述四個結論:
①水深為12尺;②蘆葦長為15尺;③![]() ;④
;④![]() .
.
其中所有正確結論的編號是( )
A.①③B.①③④C.①④D.②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com