
【題目】已知曲線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為原點,極軸為
,以極點為原點,極軸為![]() 軸非負半軸建立平面直角坐標系,直線
軸非負半軸建立平面直角坐標系,直線![]() 的參數方程為
的參數方程為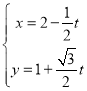 (
(![]() 為參數).
為參數).
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)在(1)中,設曲線![]() 經過伸縮變換
經過伸縮變換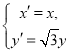 得到曲線
得到曲線![]() ,設曲線
,設曲線![]() 上任意一點為
上任意一點為![]() ,當點
,當點![]() 到直線
到直線![]() 的距離取最大值時,求此時點
的距離取最大值時,求此時點![]() 的直角坐標.
的直角坐標.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() 可將曲線
可將曲線![]() 的極坐標方程化為直角坐標方程,在直線
的極坐標方程化為直角坐標方程,在直線![]() 的參數方程中消去參數
的參數方程中消去參數![]() 可將直線
可將直線![]() 的參數方程化為普通方程;
的參數方程化為普通方程;
(2)利用伸縮變換求得曲線![]() 的普通方程,進而可得出曲線
的普通方程,進而可得出曲線![]() 的參數方程,設點
的參數方程,設點![]() ,利用點到直線的距離公式結合輔助角公式、正弦函數的有界性可求得點
,利用點到直線的距離公式結合輔助角公式、正弦函數的有界性可求得點![]() 到直線
到直線![]() 的距離的最大值,并求出對應的點
的距離的最大值,并求出對應的點![]() 的坐標.
的坐標.
(1)將曲線![]() 的極坐標方程化為
的極坐標方程化為![]() ,由
,由![]() ,
,
所以,曲線![]() 的直角坐標方程為
的直角坐標方程為![]() .
.
在直線![]() 的參數方程中消去參數
的參數方程中消去參數![]() 得
得![]() ,
,
所以,直線![]() 的普通方程為
的普通方程為![]() ;
;
(2)由伸縮變換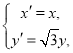 得
得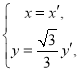 帶入圓的方程
帶入圓的方程![]() 得
得![]() ,
,
化簡得曲線![]() ,其參數方程為
,其參數方程為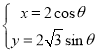 (
(![]() 為參數,且
為參數,且![]() ),
),
設點![]() ,
,
點![]() 到直線
到直線![]() 距離為:
距離為:
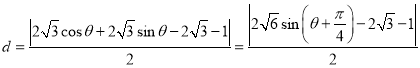 ,
,
![]() ,則
,則![]() ,所以,當
,所以,當![]() 時,即當
時,即當![]() 時,
時,
![]() 取最大值,即
取最大值,即![]() ,
,
此時,點![]() 的坐標為
的坐標為![]() .
.


科目:高中數學 來源: 題型:
【題目】孫子定理是中國古代求解一次同余式組的方法,是數論中一個重要定理,最早可見于中國南北朝時期的數學著作《孫子算經》,![]() 年英國來華傳教士偉烈亞力將其問題的解法傳至歐洲,
年英國來華傳教士偉烈亞力將其問題的解法傳至歐洲,![]() 年英國數學家馬西森指出此法符合
年英國數學家馬西森指出此法符合![]() 年由高斯得出的關于同余式解法的一般性定理,因而西方稱之為“中國剩余定理”.這個定理講的是一個關于整除的問題,現有這樣一個整除問題:將
年由高斯得出的關于同余式解法的一般性定理,因而西方稱之為“中國剩余定理”.這個定理講的是一個關于整除的問題,現有這樣一個整除問題:將![]() 至
至![]() 這
這![]() 個整數中能被
個整數中能被![]() 除余
除余![]() 且被
且被![]() 除余
除余![]() 的數按由小到大的順序排成一列構成一數列,則此數列的項數是( )
的數按由小到大的順序排成一列構成一數列,則此數列的項數是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】魚卷是泉州十大名小吃之一,不但本地人喜歡,而且深受外來游客的贊賞.小張從事魚卷生產和批發多年,有著不少來自零售商和酒店的客戶當地的習俗是農歷正月不生產魚卷,客戶正月所需要的魚卷都會在上一年農歷十二月底進行一次性采購小張把去年年底采購魚卷的數量x(單位:箱)在![]() 的客戶稱為“熟客”,并把他們去年采購的數量制成下表:
的客戶稱為“熟客”,并把他們去年采購的數量制成下表:
采購數x |
|
|
|
|
|
客戶數 | 10 | 10 | 5 | 20 | 5 |
(1)根據表中的數據作出頻率分布直方圖,并估計采購數在168箱以上(含168箱)的“熟客”人數;
(2)若去年年底“熟客”們采購的魚卷數量占小張去年年底總的銷售量的![]() ,估算小張去年年底總的銷售量(同一組中的數據用該組區間的中點值為代表);
,估算小張去年年底總的銷售量(同一組中的數據用該組區間的中點值為代表);
(3)由于魚卷受到游客們的青睞,小張做了一份市場調查,決定今年年底是否在網上出售魚卷,若不在網上出售魚卷,則按去年的價格出售,每箱利潤為20元,預計銷售量與去年持平;若在網上出售魚卷,則需把每箱售價下調2至5元,且每下調m元(![]() )銷售量可增加1000m箱,求小張今年年底收入Y(單位:元)的最大值.
)銷售量可增加1000m箱,求小張今年年底收入Y(單位:元)的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的傾斜角為
的傾斜角為![]() ,且經過點
,且經過點![]() ,以坐標原點O為極點,
,以坐標原點O為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() ,從原點O作射線交
,從原點O作射線交![]() 于點M,點N為射線OM上的點,滿足|
于點M,點N為射線OM上的點,滿足| ![]() ,記點N的軌跡為曲線C.
,記點N的軌跡為曲線C.
(1)①設動點![]() ,記
,記![]() 是直線
是直線![]() 的向上方向的單位方向向量,且
的向上方向的單位方向向量,且![]() ,以t為參數求直線
,以t為參數求直線![]() 的參數方程
的參數方程
②求曲線C的極坐標方程并化為直角坐標方程;
(2)設直線![]() 與曲線C交于P,Q兩點,求
與曲線C交于P,Q兩點,求![]() 的值
的值
查看答案和解析>>
科目:高中數學 來源: 題型:
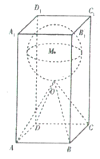
【題目】在日常生活中,石子是我們經常見到的材料,比如在各種建筑工地或者建材市場上常常能看到堆積如山的石子,它的主要成分是碳酸鈣.某雕刻師計劃在底面邊長為2m、高為4m的正四棱柱形的石料![]() 中,雕出一個四棱錐
中,雕出一個四棱錐![]() 和球M的組合體,其中O為正四棱柱的中心,當球的半徑r取最大值時,該雕刻師需去除的石料約重___________kg.(最后結果保留整數,其中
和球M的組合體,其中O為正四棱柱的中心,當球的半徑r取最大值時,該雕刻師需去除的石料約重___________kg.(最后結果保留整數,其中![]() ,石料的密度
,石料的密度![]() ,質量
,質量![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,側面ABB1A1是邊長為2的菱形,且CA=CB1.
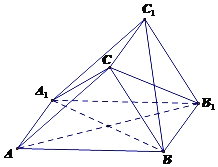
(1)證明:面CBA1⊥面CB1A;
(2)若∠BAA1=60°,A1C=BC=BA1,求點C到平面A1BC1的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com