
【題目】某市數學教研室對全市2018級15000名的高中生的學業水平考試的數學成績進行調研,隨機選取了200名高中生的學業水平考試的數學成績作為樣本進行分析,將結果列成頻率分布表如下:
數學成績 | 頻數 | 頻率 |
| 5 | 0.025 |
| 15 | 0.075 |
| 50 | 0.25 |
| 70 | 0.35 |
| 45 | 0.225 |
| 15 | 0.075 |
合計 | 200 | 1 |
根據學業水平考試的數學成績將成績分為“優秀”、“合格”、“不合格”三個等級,其中成績大于或等于80分的為“優秀”,成績小于60分的為“不合格”,其余的成績為“合格”.
(1)根據頻率分布表中的數據,估計全市學業水平考試的數學成績的眾數、中位數(精確到0.1);
(2)市數學教研員從樣本中又隨機選取了![]() 名高中生的學業水平考試的數學成績,如果這
名高中生的學業水平考試的數學成績,如果這![]() 的最小值;
的最小值;
(3)估計全市2018級高中生學業水平考試“不合格”的人數.
【答案】(1)眾數、中位數分別為75,74.3;(2)![]() 的最小值為10;(3)
的最小值為10;(3)![]() .
.
【解析】
(1)由頻率分布表中的數據,眾數為![]() ,設中位數為
,設中位數為![]() ,根據各組頻率可得
,根據各組頻率可得![]() ,解方程即可.
,解方程即可.
(2)首先求出“優秀”、“合格”、“不合格”的人數,再根據分層抽樣法可得![]() 即可.
即可.
(3)根據“不合格”的人數所占的比例即可估計出總體.
解:(1)此樣本的眾數為![]() ;
;
設中位數為![]() ,則
,則![]() ,
,
解得![]() ,所以中位數約為74.3.
,所以中位數約為74.3.
運用此樣本的數字特征,可以估計總體的數字特征,
所以全市學業水平考試的數學成績的眾數、中位數分別為75,74.3.
(2)“優秀”、“合格”、“不合格”的人數分別為60,120,20,
則“優秀”、“合格”、“不合格”的比例為3:6:1,
所以按照分層抽樣法,選取的人數為![]() ,
,
故![]() 的最小值為10.
的最小值為10.
(3)全市2018級高中生學業水平考試“不合格”的人數為![]() .
.


 計算高手系列答案
計算高手系列答案科目:高中數學 來源: 題型:
【題目】春秋以前中國已有“抱甕而出灌”的原始提灌方式,使用提水吊桿——桔槔,后發展成轆轤.19世紀末,由于電動機的發明,離心泵得到了廣泛應用,為發展機械提水灌溉提供了條件.圖形如圖所示為灌溉抽水管道在等高圖的上垂直投影,在A處測得B處的仰角為37度,在A處測得C處的仰角為45度,在B處測得C處的仰角為53度,A點所在等高線值為20米,若BC管道長為50米,則B點所在等高線值為( )(參考數據![]() )
)
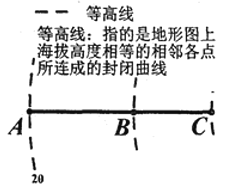
A.30米B.50米C.60米D.70米
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了保障某種藥品的主要藥理成分在國家藥品監督管理局規定的值范圍內,某制藥廠在該藥品的生產過程中,檢驗員在一天中按照規定每間隔2小時對該藥品進行檢測,每天檢測4次:每次檢測由檢驗員從該藥品生產線上隨機抽取20件產品進行檢測,測量其主要藥理成分含量(單位:![]() )根據生產經驗,可以認為這條藥品生產線正常狀態下生產的產品的其主要藥理成分含量服從正態分布
)根據生產經驗,可以認為這條藥品生產線正常狀態下生產的產品的其主要藥理成分含量服從正態分布![]() .
.
(1)假設生產狀態正常,記![]() 表示某次抽取的20件產品中其主要藥理成分含量在
表示某次抽取的20件產品中其主要藥理成分含量在![]() 之外的藥品件數,求
之外的藥品件數,求![]() 的數學期望;
的數學期望;
(2)在一天的四次檢測中,如果有一次出現了主要藥理成分含量在![]() 之外的藥品,就認為這條生產線在這一天的生產過程可能出現異常情況,需對本次的生產過程進行檢查;如果有兩次或兩次以上出現了主要藥理成分含量在
之外的藥品,就認為這條生產線在這一天的生產過程可能出現異常情況,需對本次的生產過程進行檢查;如果有兩次或兩次以上出現了主要藥理成分含量在![]() 之外的藥品,則需停止生產并對原材料進行檢測.
之外的藥品,則需停止生產并對原材料進行檢測.
①下面是檢驗員在某次抽取的20件藥品的主要藥理成分含量:
10.02 | 9.78 | 10.04 | 9.92 | 10.14 | 9.22 | 10.13 | 9.91 | 9.95 |
10.09 | 9.96 | 9.88 | 10.01 | 9.98 | 10.05 | 10.05 | 9.96 | 10.12 |
經計算得,![]() ,
, .其中
.其中![]() 為抽取的第
為抽取的第![]() 件藥品的主要藥理成分含量
件藥品的主要藥理成分含量![]() ,用樣本平均數
,用樣本平均數![]() 作為
作為![]() 的估計值
的估計值![]() ,用樣本標準差
,用樣本標準差![]() 作為
作為![]() 的估計值
的估計值![]() ,利用估計值判斷是否需對本次的生產過程進行檢查?
,利用估計值判斷是否需對本次的生產過程進行檢查?
②試確定一天中需停止生產并對原材料進行檢測的概率(精確到0.001).
附:若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐PABC中,![]() 底面ABC,
底面ABC,![]() ,
,![]() ,
,![]() ,D,E分別是AC,PC的中點,F是PB上一點,且
,D,E分別是AC,PC的中點,F是PB上一點,且![]() ,M為PA的中點,二面角
,M為PA的中點,二面角![]() 的大小為45°.
的大小為45°.

(1)證明:![]() 平面AEF;
平面AEF;
(2)求直線AF與平面BCM所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校對高一年級學生寒假參加社區服務的次數進行了統計,隨機抽取了![]() 名學生作為樣本,得到這
名學生作為樣本,得到這![]() 名學生參加社區服務的次數,根據此數據作出了頻率分布統計表和頻率分布直方圖如下:
名學生參加社區服務的次數,根據此數據作出了頻率分布統計表和頻率分布直方圖如下:

(1)求表中![]() 的值和頻率分布直方圖中
的值和頻率分布直方圖中![]() 的值,并根據頻率分布直方圖估計該校高一學生寒假參加社區服務次數的中位數;
的值,并根據頻率分布直方圖估計該校高一學生寒假參加社區服務次數的中位數;
(2)如果用分層抽樣的方法從樣本服務次數在![]() 和
和![]() 的人中共抽取6人,再從這6人中選2人,求2人服務次數都在
的人中共抽取6人,再從這6人中選2人,求2人服務次數都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】孫子定理是中國古代求解一次同余式組的方法,是數論中一個重要定理,最早可見于中國南北朝時期的數學著作《孫子算經》,![]() 年英國來華傳教士偉烈亞力將其問題的解法傳至歐洲,
年英國來華傳教士偉烈亞力將其問題的解法傳至歐洲,![]() 年英國數學家馬西森指出此法符合
年英國數學家馬西森指出此法符合![]() 年由高斯得出的關于同余式解法的一般性定理,因而西方稱之為“中國剩余定理”.這個定理講的是一個關于整除的問題,現有這樣一個整除問題:將
年由高斯得出的關于同余式解法的一般性定理,因而西方稱之為“中國剩余定理”.這個定理講的是一個關于整除的問題,現有這樣一個整除問題:將![]() 至
至![]() 這
這![]() 個整數中能被
個整數中能被![]() 除余
除余![]() 且被
且被![]() 除余
除余![]() 的數按由小到大的順序排成一列構成一數列,則此數列的項數是( )
的數按由小到大的順序排成一列構成一數列,則此數列的項數是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】光伏發電是利用太陽能電池及相關設備將太陽光能直接轉化為電能.近幾年在國內出臺的光伏發電補貼政策的引導下,某地光伏發電裝機量急劇上漲,如下表:
年份 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
年份代碼 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
新增光伏裝機量 | 0.4 | 0.8 | 1.6 | 3.1 | 5.1 | 7.1 | 9.7 | 12.2 |
某位同學分別用兩種模型:①![]() ,②
,②![]() 進行擬合,得到相應的回歸方程并進行殘差分析,殘差圖如下(注:殘差等于
進行擬合,得到相應的回歸方程并進行殘差分析,殘差圖如下(注:殘差等于![]() ):
):

經過計算得![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
(1)根據殘差圖,比較模型①,②的擬合效果,應該選擇哪個模型?并簡要說明理由.
(2)根據(1)的判斷結果及表中數據建立![]() 關于
關于![]() 的回歸方程,并預測該地區2020年新增光伏裝機量是多少.(在計算回歸系數時精確到0.01)
的回歸方程,并預測該地區2020年新增光伏裝機量是多少.(在計算回歸系數時精確到0.01)
附:回歸直線的斜率和截距的最小二乘估計公式分別為: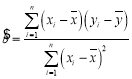 ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com