
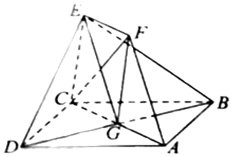
 (理)如圖,正方形ABCD和四邊形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.
(理)如圖,正方形ABCD和四邊形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.分析 (Ⅰ)設AC與BD交于點G,則在平面BDE中,可以先證明四邊形AGEF為平行四邊形,得到EG∥AF,就可證:AF∥平面BDE;
(Ⅱ)連接FG,可得平行四邊形CEFG為菱形,求出CF⊥EG,又四邊形ABCD為正方形,可得BD⊥AC,進一步求出BD⊥平面ACEF,就可以得到CF⊥平面BDE;
(Ⅲ)如圖建立空間直角坐標系,由(II)知,$\overrightarrow{CF}$是平面BDE的一個法向量,再利用平面ABE的法向量n•$\overrightarrow{BA}$=0,n$•\overrightarrow{BE}$=0,求出平面ABE的法向量$\overrightarrow{n}$,就可以求出二面角A-BE-D的大小.
解答 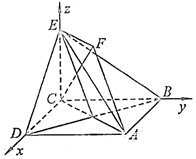 (Ⅰ)證明:設AC于BD交于點G,
(Ⅰ)證明:設AC于BD交于點G,
∵EF∥AG,且EF=1,AG=$\frac{1}{2}$AC=1,
∴四邊形AGEF為平行四邊形,
∴AF∥EG.
∵EG?面BDE,AF?平面BDE,
∴AF∥平面BDE;
(Ⅱ)證明:連接FG,∵EF∥CG,EF=CG=CE,∴平行四邊形CEFG為菱形,∴CF⊥EG.
∵四邊形ABCD為正方形,∴BD⊥AC.
又∵平面ACEF⊥平面ABCD,且平面ACEF∩平面ABCD=AC,
∴BD⊥平面ACEF.
∴CF⊥BD.又BD∩EG=G,
∴CF⊥平面BDE;
(III)解:令EF=CE=1,則AB=$\sqrt{2}$.如圖建立空間直角坐標系.
由(II)知,$\overrightarrow{CF}$=($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$,1)是平面BDE的一個法向量.
設平面ABE的法向量$\overrightarrow{n}$=(x,y,z),則n•$\overrightarrow{BA}$=0,n$•\overrightarrow{BE}$=0.
即$\left\{\begin{array}{l}{(x,y,z)•(\sqrt{2},0.0)}\\{(x,y,z)•(0.-\sqrt{2},0)}\end{array}\right.$,
∴x=0,且z=$\sqrt{2}$y.令y=1,則z=$\sqrt{2}$.
∴n=(0,1,$\sqrt{2}$).
從而cos(n,$\overrightarrow{CF}$)=$\frac{n•\overrightarrow{CF}}{|n||\overrightarrow{CF}|}$=$\frac{\sqrt{3}}{2}$.
∵二面角A-BE-D為銳角,
∴二面角A-BE-D的大小為$\frac{π}{6}$.
點評 本題考查直線和平面垂直的判定和性質和線面平行的推導以及二面角的求法,在證明線面平行時,其常用方法是在平面內找已知直線平行的直線,當然也可以用面面平行來推導線面平行,是中檔題.


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | 2$\sqrt{2}$ | B. | 5 | C. | 3 | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 第Ⅰ象限 | B. | 第Ⅱ象限 | C. | 第Ⅲ象限 | D. | 第Ⅳ象限 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [1,+∞) | B. | (1,+∞) | C. | (-∞,1] | D. | (-∞,1) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com