
【題目】如圖,三棱柱![]() 的側面
的側面![]() 是邊長為1的正方形,側面
是邊長為1的正方形,側面![]() 側面
側面![]() 是
是![]() 的中點.
的中點.

(1)求證:![]() 平面
平面![]() ;
;
(2)求證:![]() 平面
平面![]() ;
;
(3)在線段![]() 上是否存在一點
上是否存在一點![]() ,使二面角
,使二面角![]() 為45°,若存在,求
為45°,若存在,求![]() 的長;若不存在,說明理由.
的長;若不存在,說明理由.
【答案】(1)證明見解析;(2)證明見解析;(3)存在,![]() .
.
【解析】
試題分析:(1)根據線面平行的判定定理即可證明![]() 平面
平面![]() ;(2)根據線面垂直的判定定理即可證明
;(2)根據線面垂直的判定定理即可證明![]() 平面
平面![]() ;(3)在建立空間直角坐標系,利用向量法結合二面角的大小建立方程關系即可得到結論.
;(3)在建立空間直角坐標系,利用向量法結合二面角的大小建立方程關系即可得到結論.
試題解析:(1)證明:連接![]() 與
與![]() 相交于
相交于![]() ,則
,則![]() 為
為![]() 的中點,連接
的中點,連接![]() ,
,
因為![]() 為
為![]() 的中點,所以
的中點,所以![]() .
.
因為![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
(2)證明:![]() ,在
,在![]() 中,
中,![]() .
.
因為![]() ,所以
,所以![]() ,
,
因為側面![]() 側面
側面![]() ,側面
,側面![]() 側面
側面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]()
(3)解:
![]() 兩兩互相垂直,建立空間直角坐標系
兩兩互相垂直,建立空間直角坐標系![]() ,
,
假設在線段![]() 上存在一點
上存在一點![]() ,使二面角
,使二面角![]() 為
為![]() ,
,
平面![]() 的法向量
的法向量![]() ,設
,設![]() ,
,![]() .
.
所以![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
則 ,所以
,所以 ,
,
令![]() ,得
,得![]() ,所以
,所以![]() 的法向量為
的法向量為![]() .
.
因為![]() ,所以
,所以![]() ,解得
,解得![]() ,故
,故![]() ,
,
因此在線段![]() 上存在一點
上存在一點![]() ,使二面角
,使二面角![]() 為
為![]() ,且
,且![]()



科目:高中數學 來源: 題型:
【題目】(1)求過直線l1:x-2y+3=0與直線l2:2x+3y-8=0的交點,且到點P(0,4)的距離為2的直線方程.
(2)設直線l的方程為(a+1)x+y+2-a=0(a∈R).若l在兩坐標軸上的截距相等,求l的方程;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一船由西向東航行,在A處測得某島M的方位角為α,前進5km后到達B處,測得島M的方位角為β.已知該島周圍3km內有暗礁,現該船繼續東行.
(1)若α=2β=60°,問該船有無觸礁危險?
(2)當α與β滿足什么條件時,該船沒有觸礁的危險?
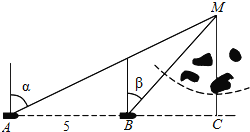
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為迎接春節,某工廠大批生產小孩具—— 拼圖,工廠為了規定工時定額,需要確定加工拼圖所花費的時間,為此進行了10次試驗,測得的數據如下:
拼圖數
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
加工時間
| 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(1)畫出散點圖,并判斷![]() 與
與![]() 是否具有線性相關關系;
是否具有線性相關關系;

(2)求回歸方程;
(3)根據求出的回歸方程,預測加工2010個拼圖需要用多少小時?(精確到0.1)
附:回歸直線的斜率和截距的最小二乘估計公式分別為:
 ,
, ![]() .
.
參考數據 | 合計 | ||||||||||
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 550 |
| 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 | 917 |
| 100 | 400 | 900 | 1600 | 2500 | 3600 | 4900 | 6400 | 8100 | 10000 | 38500 |
| 620 | 1360 | 2250 | 3240 | 4450 | 5700 | 7140 | 8840 | 10350 | 12200 | 55950 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場預計全年分批購入每臺2000元的電視機共3600臺.每批都購入![]() 臺(
臺(![]() 是自然數)且每批均需付運費400元.貯存購入的電視機全年所需付的保管費 與每批購入電視機的總價值(不含運費)成正比.若每批購入400臺,則全年需用去運輸和保管總費用43600元.現在全年只有24000元資金可以支付這筆費用,請問,能否恰當安排每批進貨數量,使資金夠用?寫出你的結論,并說明理由.
是自然數)且每批均需付運費400元.貯存購入的電視機全年所需付的保管費 與每批購入電視機的總價值(不含運費)成正比.若每批購入400臺,則全年需用去運輸和保管總費用43600元.現在全年只有24000元資金可以支付這筆費用,請問,能否恰當安排每批進貨數量,使資金夠用?寫出你的結論,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com