
【題目】在平面直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 與直線
與直線![]() 的直角坐標方程.
的直角坐標方程.
(2)直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,與曲線
,與曲線![]() 的交點為
的交點為![]() ,
,![]() ,求
,求![]() 的值.
的值.
 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,傾斜角為
中,傾斜角為![]() 的直線
的直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).在以坐標原點為極點,
為參數).在以坐標原點為極點,![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的傾斜角.
的傾斜角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在①![]() ;②
;②![]() 這兩個條件中任選-一個,補充在下面問題中,然后解答補充完整的題.
這兩個條件中任選-一個,補充在下面問題中,然后解答補充完整的題.

在![]() 中,角
中,角![]() 的對邊分別為
的對邊分別為![]() ,已知 ,
,已知 ,![]() .
.
(1)求![]() ;
;
(2)如圖,![]() 為邊
為邊![]() 上一點,
上一點,![]() ,求
,求![]() 的面積
的面積
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某汽車品牌為了解客戶對其旗下的五種型號汽車的滿意情況,隨機抽取了一些客戶進行回訪,調查結果如下表:
汽車型號 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
回訪客戶(人數) | 250 | 100 | 200 | 700 | 350 |
滿意率 | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
滿意率是指某種型號汽車的回訪客戶中,滿意人數與總人數的比值.假設客戶是否滿意互相獨立,且每種型號汽車客戶對于此型號汽車滿意的概率與表格中該型號汽車的滿意率相等.
(1)從所有的回訪客戶中隨機抽取1人,求這個客戶滿意的概率;
(2)從Ⅰ型號和Ⅴ型號汽車的所有客戶中各隨機抽取1人,設其中滿意的人數為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第7屆世界軍人運動會于2019年10月18日至27日在湖北武漢舉行,賽期10天,共設置射擊、游泳、田徑、籃球等27個大項,329個小項.共有來自100多個國家的近萬名現役軍人同臺競技.前期為迎接軍運會順利召開,武漢市很多單位和部門都開展了豐富多彩的宣傳和教育活動,努力讓大家更多的了解軍運會的相關知識,并倡議大家做文明公民.武漢市體育局為了解廣大民眾對軍運會知識的知曉情況,在全市開展了網上問卷調查,民眾參與度極高,現從大批參與者中隨機抽取200名幸運參與者,他們得分(滿分100分)數據,統計結果如下:
組別 |
|
|
|
|
|
|
|
頻數 | 5 | 30 | 40 | 50 | 45 | 20 | 10 |
(1)若此次問卷調查得分整體服從正態分布,用樣本來估計總體,設![]() ,
,![]() 分別為這200人得分的平均值和標準差(同一組數據用該區間中點值作為代表),求
分別為這200人得分的平均值和標準差(同一組數據用該區間中點值作為代表),求![]() ,
,![]() 的值(
的值(![]() ,
,![]() 的值四舍五入取整數),并計算
的值四舍五入取整數),并計算![]() ;
;
(2)在(1)的條件下,為感謝大家參與這次活動,市體育局還對參加問卷調查的幸運市民制定如下獎勵方案:得分低于![]() 的可以獲得1次抽獎機會,得分不低于
的可以獲得1次抽獎機會,得分不低于![]() 的可獲得2次抽獎機會,在一次抽獎中,抽中價值為15元的紀念品A的概率為
的可獲得2次抽獎機會,在一次抽獎中,抽中價值為15元的紀念品A的概率為![]() ,抽中價值為30元的紀念品B的概率為
,抽中價值為30元的紀念品B的概率為![]() .現有市民張先生參加了此次問卷調查并成為幸運參與者,記Y為他參加活動獲得紀念品的總價值,求Y的分布列和數學期望,并估算此次紀念品所需要的總金額.
.現有市民張先生參加了此次問卷調查并成為幸運參與者,記Y為他參加活動獲得紀念品的總價值,求Y的分布列和數學期望,并估算此次紀念品所需要的總金額.
(參考數據:![]() ;
;![]() ;
;![]() .)
.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正方形![]() ,
,![]() 分別是
分別是![]() 的中點,將
的中點,將![]() 沿
沿![]() 折起,如圖所示,記二面角
折起,如圖所示,記二面角![]() 的大小為
的大小為![]()
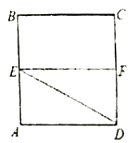
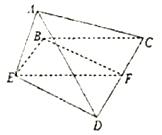
(1)證明:![]()
(2)若![]() 為正三角形,試判斷點
為正三角形,試判斷點![]() 在平面
在平面![]() 內的身影
內的身影![]() 是否在直線
是否在直線![]() 上,證明你的結論,并求角
上,證明你的結論,并求角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年冬,北京霧霾天數明顯減少,據環保局統計三個月的空氣質量,達到優良的天數超過![]() 天,重度污染的天數僅有
天,重度污染的天數僅有![]() 天,主要原因是政府對治理霧霾采取有效措施.如:(1)減少機動車尾氣排放(2)實施煤改電或煤改氣工程(3)關停了大量的排污企業(4)部分企業季節性停產.為了解農村地區實施煤改氣工程后天然氣的使用從某鄉鎮隨機抽取
天,主要原因是政府對治理霧霾采取有效措施.如:(1)減少機動車尾氣排放(2)實施煤改電或煤改氣工程(3)關停了大量的排污企業(4)部分企業季節性停產.為了解農村地區實施煤改氣工程后天然氣的使用從某鄉鎮隨機抽取![]() 戶,進行月均用氣量調查,得到的用氣量數據均在區間
戶,進行月均用氣量調查,得到的用氣量數據均在區間![]() 內,表如下
內,表如下
分組 | 頻數 | 頻率 |
| 14 | 0.14 |
|
|
|
| 55 | 0.55 |
| 4 | 0.04 |
| 2 | 0.02 |
合計 | 100 | 1 |
(1)求![]() 和
和![]() 值,若同組內的每個數據用該組區間中點值代替,估計該鄉鎮每戶平均用氣量;
值,若同組內的每個數據用該組區間中點值代替,估計該鄉鎮每戶平均用氣量;
(2)從樣本調查的用氣量![]() 和
和![]() 的用戶組中任選2戶,進行燃氣使用滿意度調查,求2戶用氣量處于不同區間的概率.
的用戶組中任選2戶,進行燃氣使用滿意度調查,求2戶用氣量處于不同區間的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com