
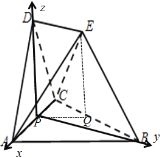
【題目】如圖,空間幾何體![]() ,△
,△![]() 、△
、△![]() 、△
、△![]() 均是邊長為2的等邊三角形,平面
均是邊長為2的等邊三角形,平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,![]() 為
為![]() 中點.
中點.

(1)證明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)詳見解析(2)![]()
【解析】
(1)分別取![]() ,
,![]() 中點
中點![]() ,
,![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,通過面面平行的判定定理,證得面
,通過面面平行的判定定理,證得面![]() 面
面![]() ,從而證得
,從而證得![]() 平面
平面![]() .(2)方法一(向量法):以點
.(2)方法一(向量法):以點![]() 為原點,以
為原點,以![]() 為
為![]() 軸,以
軸,以![]() 為
為![]() 軸,以
軸,以![]() 為
為![]() 軸,建立空間直角坐標系,利用平面
軸,建立空間直角坐標系,利用平面![]() 和平面
和平面![]() 的法向量,計算二面角的余弦值.方法二(幾何法):過
的法向量,計算二面角的余弦值.方法二(幾何法):過![]() 點作
點作![]() 垂線,垂足為
垂線,垂足為![]() ,連接
,連接![]() .由此作出二面角的平面角
.由此作出二面角的平面角![]() 并證明,解直角三角形求得二面角的余弦值.
并證明,解直角三角形求得二面角的余弦值.
(1)分別取![]() ,
,![]() 中點
中點![]() ,
,![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
由面![]() 面
面![]() 且交于
且交于![]() ,
,![]() 平面
平面![]() ,
,![]() 有
有![]() 面
面![]()
由面![]() 面
面![]() 且交于
且交于![]() ,
,![]() 平面
平面![]() ,
,![]() 有
有![]() 面
面![]()
所以![]() ,
,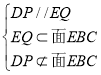 ,所以
,所以![]() ,
,
由![]() 有
有![]() ,
,
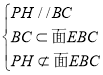 ,所以
,所以![]() ,
,
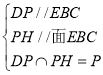 ,所以面
,所以面![]() 面
面![]() ,所以
,所以![]()

(2)
法1:以點![]() 為原點,以
為原點,以![]() 為
為![]() 軸,以
軸,以![]() 為
為![]() 軸,以
軸,以![]() 為
為![]() 軸,建立如圖所示空間直角坐標系
軸,建立如圖所示空間直角坐標系
由![]() 面
面![]() ,所以面
,所以面![]() 的法向量可取
的法向量可取![]()
點![]() ,點
,點![]() ,點
,點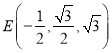 ,
,
![]() ,
,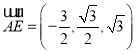 ,
,
設面![]() 的法向量
的法向量![]() ,所以
,所以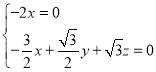 ,取
,取![]()
設二面角![]() 的平面角為
的平面角為![]() ,據判斷其為銳角.
,據判斷其為銳角.

法2:過![]() 點作
點作![]() 垂線,垂足為
垂線,垂足為![]() ,連接
,連接![]() .
.
由(1)問可知![]() 又因為
又因為![]() ,所以
,所以![]() 平面
平面![]() ,則有
,則有![]() .
.
所以![]() 為二面角
為二面角![]() 的平面角.
的平面角.
由題可知![]() ,所以
,所以![]() ,則
,則![]()
所以,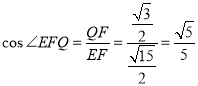


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 與直線
與直線![]() 的直角坐標方程.
的直角坐標方程.
(2)直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,與曲線
,與曲線![]() 的交點為
的交點為![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國剪紙是一種用剪刀或刻刀在紙上剪刻花紋,用于裝點生活或配合其他民俗活動的民間藝術;蘊含了極致的數學美和豐富的傳統文化信息,現有一幅剪紙的設計圖,其中的4個小圓均過正方形的中心,且內切于正方形的兩鄰邊.若在正方形內隨機取一點,則該點取自黑色部分的概率為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.

(1)證明:![]() 平面
平面![]() ;
;
(2)在線段![]() 上,是否存在一點
上,是否存在一點![]() ,使得二面角
,使得二面角![]() 的大小為
的大小為![]() ?如果存在,求
?如果存在,求![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點為
的焦點為![]() ,
,![]() 軸上方的點
軸上方的點![]() 在拋物線上,且
在拋物線上,且![]() ,直線
,直線![]() 與拋物線交于
與拋物線交于![]() ,
,![]() 兩點(點
兩點(點![]() ,
,![]() 與
與![]() 不重合),設直線
不重合),設直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() .
.
(Ⅰ)求拋物線的方程;
(Ⅱ)當![]() 時,求證:直線
時,求證:直線![]() 恒過定點并求出該定點的坐標.
恒過定點并求出該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD-ABCD中,平面![]() 垂直于對角線AC,且平面
垂直于對角線AC,且平面![]() 截得正方體的六個表面得到截面六邊形,記此截面六邊形的面積為S,周長為l,則( )
截得正方體的六個表面得到截面六邊形,記此截面六邊形的面積為S,周長為l,則( )
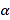
A. S為定值,l不為定值 B. S不為定值,l為定值
C. S與l均為定值 D. S與l均不為定值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數![]()
(1)![]() 是
是![]() 的極小值點;
的極小值點;
(2)函數![]() 有且只有1個零點;
有且只有1個零點;
(3)![]() 恒成立;
恒成立;
(4)設函數![]() ,若存在區間
,若存在區間![]() ,使
,使![]() 在
在![]() 上的值域是
上的值域是![]() ,則
,則![]() .
.
上述說法正確的序號為_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設一個袋子里有紅、黃、藍色小球各一個現每次從袋子里取出一個球(取出某色球的概率均相同),確定顏色后放回,直到連續兩次均取出紅色球時為止,記此時取出球的次數為ξ,則ξ的數學期望為_____ .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的最小正周期為
的最小正周期為![]() ,其圖象關于直線
,其圖象關于直線![]() 對稱.給出下面四個結論:①將
對稱.給出下面四個結論:①將![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度后得到函數圖象關于原點對稱;②點
個單位長度后得到函數圖象關于原點對稱;②點![]() 為
為![]() 圖象的一個對稱中心;③
圖象的一個對稱中心;③![]() ;④
;④![]() 在區間
在區間![]() 上單調遞增.其中正確的結論為( )
上單調遞增.其中正確的結論為( )
A.①②B.②③C.②④D.①④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com