(本題滿分14分)在邊長為3的正三角形ABC中,E、F、P分別是AB、AC、BC邊上的點(diǎn),滿足
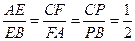
,將
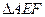
沿EF折起到
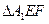
的位置,使二面角
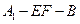
成直二面角,連結(jié)
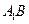
,
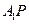
(如圖)(I)求證:
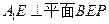
(Ⅱ)求點(diǎn)B到面
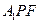
的距離(Ⅲ)求異面直線BP與
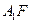
所成角的余弦
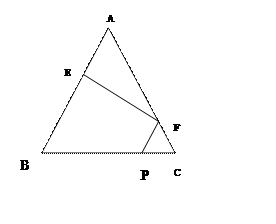

(Ⅰ)見解析 (Ⅱ)
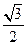
(Ⅲ)
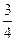
(I)在圖1中,取BE的中點(diǎn)D,連DF
∵
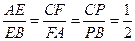
,∵
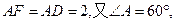
∴
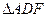
為正三角形
又∵AE="ED=1 " ∴
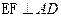
∴在圖2中有
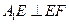
,
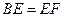
∴

為二面角
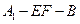
的平面角
∵二面角
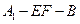
為直二面角 ∴
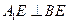
又∵
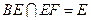
∴
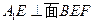
即
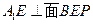
…………5分
(Ⅱ)∵BE//PF ∴BE//面
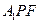
∵B到面
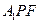
的距離即為E到面
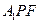
的距離,
∵
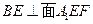
,又BE//PF,∴
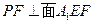
∴
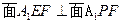
∵E到面
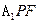
的距離即為
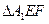
中E到
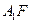
的距離
d=A
1E×
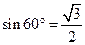
∴點(diǎn)B到面
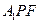
的距離為
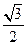
………………10分
(Ⅲ)∵DF//BP ∴
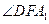
即為所求角
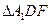
中
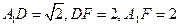
,
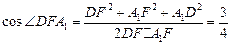
∴異面直線BP與
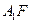
所成角的余弦值為
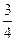
………………14分
法二:(建立空間直角坐標(biāo)系,略解)
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
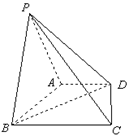
如圖,在四棱錐
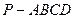
中,底面
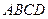
是直角梯形,
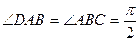
,且
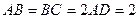
,側(cè)面
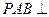
底面
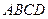
,
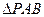
是等邊三角形.
(1)求證:
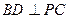
;
(2)求二面角
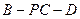
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
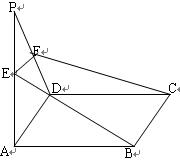
如圖,四邊形ABCD是矩形,
面ABCD,過BC作平面BCFE交AP于E,
交DP于F,求證:四邊形BCFE是梯形
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
在正方體
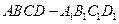
中,
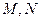
分別是
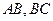
中點(diǎn).
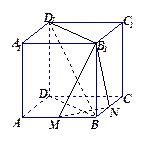
(Ⅰ)求證:平面
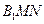
⊥平面
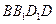
;
(Ⅱ)若在棱
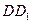
上有一點(diǎn)
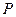
,使
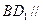
平面
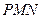
,求
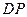
與
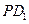
的比.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
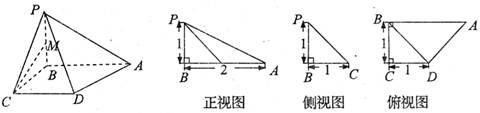
(1)設(shè)PB的中點(diǎn)為M,求證CM是否平行于平面PDA?
(2)在BC邊上是否存在點(diǎn)Q,使得二面角A—PD—Q為120°?若存在,確定點(diǎn)Q的位置;若不存在,請說明理由
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
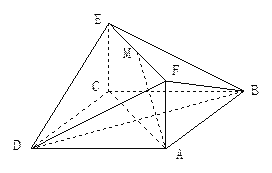
如圖,已知正方形
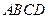
和矩形
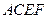
所在的平面互相垂直,
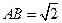
,
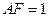
,
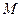
是線段
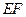
的中點(diǎn).
(Ⅰ)求三棱錐
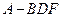
的體積;
(Ⅱ)求證:
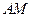
//平面
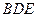
;
(Ⅲ)求異面直線
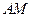
與
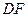
所成的角.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
用一張長為8 cm,寬為4 cm的矩形硬紙卷成圓柱的側(cè)面,求圓柱的軸截面的面積與底面積.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,已知斜三棱柱
ABC-A1B1C1的底面△
ABC為直角三角形,∠
C=90°,側(cè)棱與底面成60°角,點(diǎn)
B1在底面的射影
D為
BC的中點(diǎn).

求證:
AC⊥平面
BCC1B
1.
查看答案和解析>>

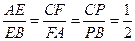 ,將
,將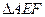 沿EF折起到
沿EF折起到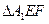 的位置,使二面角
的位置,使二面角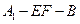 成直二面角,連結(jié)
成直二面角,連結(jié)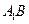 ,
,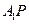 (如圖)(I)求證:
(如圖)(I)求證: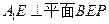 (Ⅱ)求點(diǎn)B到面
(Ⅱ)求點(diǎn)B到面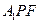 的距離(Ⅲ)求異面直線BP與
的距離(Ⅲ)求異面直線BP與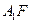 所成角的余弦
所成角的余弦

 閱讀快車系列答案
閱讀快車系列答案


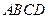 和矩形
和矩形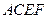 所在的平面互相垂直,
所在的平面互相垂直,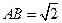 ,
,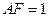 ,
,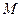 是線段
是線段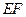 的中點(diǎn).
的中點(diǎn).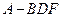 的體積;
的體積;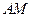 //平面
//平面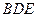 ;
;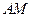 與
與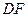 所成的角.
所成的角.