
分析 求函數的導數,利用導數研究函數的單調性和最值,建立條件關系進行求解即可.
解答 解:設f(x)=lnx-x+1+a,當x∈[$\frac{1}{e}$,1]時,f′(x)=$\frac{1-x}{x}$>0,f(x)是增函數,
∴x∈[$\frac{1}{e}$,1]時,f(x)∈[a-$\frac{1}{e}$,a],
∵對任意的x1∈[$\frac{1}{e}$,1],總存在x2∈[0,1],使得lnx-x+1+a=x2ex成立,
∴[a-$\frac{1}{e}$,a]是g(x)的不含極值點的單值區間的子集,
∵g′(x)=x(2+x)ex,∴x∈(0,1],g′(x)>0,g(x)=x2ex是增函數,
∴g(x)⊆[0,e]
∴[a-$\frac{1}{e}$,a]⊆[0,e],
∴$\frac{1}{e}$≤a≤e;
故答案為$\frac{1}{e}$≤a≤e.
點評 本題主要考查方程恒成立問題,構造函數,求函數的導數,利用導數研究函數的單調性和取值范圍是解決本題的關鍵.


 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數學 來源: 題型:選擇題
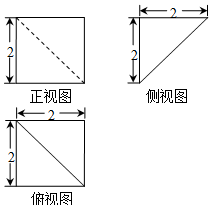
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 是否愿意提供志愿者服務 性別 | 愿意 | 不愿意 |
| 男生 | 30 | 10 |
| 女生 | 20 | 20 |
| P(K2≥k0) | 0.025 | 0.010 |
| k0 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 向右平移$\frac{π}{4}$個單位長度 | B. | 向右平移$\frac{π}{12}$個單位長度 | ||
| C. | 向左平移$\frac{π}{4}$個單位長度 | D. | 向左平移$\frac{π}{12}$個單位長度 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
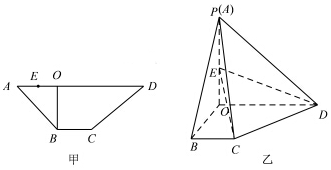
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
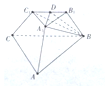 已知三棱臺ABC-A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6
已知三棱臺ABC-A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
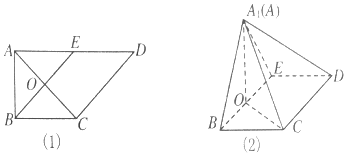
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com