
【題目】一青蛙從點![]() 開始依次水平向右和豎直向上跳動,其落點坐標依次是
開始依次水平向右和豎直向上跳動,其落點坐標依次是![]()
![]() ,(如圖所示,
,(如圖所示,![]() 坐標以已知條件為準),
坐標以已知條件為準),![]() 表示青蛙從點
表示青蛙從點![]() 到點
到點![]() 所經過的路程.
所經過的路程.

(1)若點![]() 為拋物線
為拋物線![]() (
(![]() )準線上一點,點
)準線上一點,點![]() 均在該拋物線上,并且直線
均在該拋物線上,并且直線![]() 經過該拋物線的焦點,證明
經過該拋物線的焦點,證明![]() .
.
(2)若點![]() 要么落在
要么落在![]() 所表示的曲線上,要么落在
所表示的曲線上,要么落在![]() 所表示的曲線上,并且
所表示的曲線上,并且![]() ,試寫出
,試寫出![]() (不需證明);
(不需證明);
(3)若點![]() 要么落在
要么落在![]() 所表示的曲線上,要么落在
所表示的曲線上,要么落在![]() 所表示的曲線上,并且
所表示的曲線上,并且![]() ,求
,求![]() 的表達式.
的表達式.
【答案】解:(1)設![]() ,由于青蛙依次向右向上跳動,
,由于青蛙依次向右向上跳動,
所以![]() ,
,![]() ,由拋物線定義知:
,由拋物線定義知:![]()
![]()
![]() 分
分
(2) 依題意,![]()
![]()
![]()
![]()
隨著![]() 的增大,點
的增大,點![]() 無限接近點
無限接近點![]()
![]() 分
分
橫向路程之和無限接近![]() ,縱向路程之和無限接近
,縱向路程之和無限接近![]()
![]() 分
分
所以![]() =
=![]()
![]() 分
分
(3)方法一:設點![]() ,由題意,
,由題意,![]() 的坐標滿足如下遞推關系:
的坐標滿足如下遞推關系:![]() ,且
,且![]()
其中![]()
![]() 分
分
∴![]() ,即
,即![]() ,
,
∴![]() 是以
是以![]() 為首項,
為首項,![]() 為公差的等差數列,
為公差的等差數列,
∴![]() ,
,
所以當![]() 為偶數時,
為偶數時,![]() ,于是
,于是![]() ,
,
又![]()
∴當![]() 為奇數時,
為奇數時,![]()
![]() 分
分
當![]() 為偶數時,
為偶數時,
![]()
![]()
![]()
![]()
當![]() 為奇數時,
為奇數時,
![]()
![]()
![]()
![]()
所以,當![]() 為偶數時,
為偶數時,![]()
當![]() 為奇數時,
為奇數時,![]()
所以,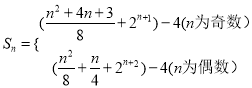
![]() 分
分
方法二:由題意知![]()
其中![]()
![]()
觀察規律可知:下標為奇數的點的縱坐標為首項為![]() ,公比為
,公比為![]() 的等比數列.相鄰橫坐標之差為首項為2,公差為1的等差數列.下標為偶數的點也有此規律.并由數學歸納法可以證明.
的等比數列.相鄰橫坐標之差為首項為2,公差為1的等差數列.下標為偶數的點也有此規律.并由數學歸納法可以證明.![]() 分
分
所以,當![]() 為偶數時,
為偶數時,![]()
當![]() 為奇數時,
為奇數時,![]()
當![]() 為偶數時,
為偶數時,![]()
當![]() 為奇數時,
為奇數時,![]()
![]() 分
分
所以,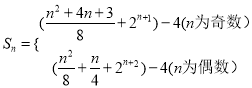
![]() 分
分
【解析】
試題(1)直接借助題設求解即可獲證;(2)運用題設條件和極限思想表示出來再求解即可;(3)運用題設中提供的信息分類進行求解.
試題解析:(1)設![]() ,由于青蛙依次向右向上跳動,
,由于青蛙依次向右向上跳動,
所以![]() ,
,![]() ,由拋物線定義知:
,由拋物線定義知:![]() .
.
(2)依題意,![]() ,
,![]() ,
,![]() (
(![]() )
)
![]()
![]()
![]()
隨著![]() 的增大,點
的增大,點![]() 無限接近點
無限接近點![]() ,
,
橫向路程之和無限接近![]() ,縱向路程之和無限接近
,縱向路程之和無限接近![]() ,
,
所以![]() .
.
(3)方法一:設點![]() ,則題意,
,則題意,![]() 的坐標滿足如下遞推關系:
的坐標滿足如下遞推關系:
![]() ,且
,且![]() ,
,![]() (
(![]() )
)
其中![]() ,
,![]()
∴![]() ,即
,即![]() ,
,
∴![]() 是以
是以![]() 為首項,2為公差的等差數列,
為首項,2為公差的等差數列,
∴![]() ,
,
所以當![]() 為偶數時,
為偶數時,![]() ,于是
,于是![]() ,
,
又![]() ,
,
∴當![]() 為奇數時,
為奇數時,![]() ,
,![]() ,
,
當![]() 為偶數時,
為偶數時,
![]()
![]()
![]()
![]()
當![]() 為奇數時,
為奇數時,
![]()
![]()
![]()
![]()
所以,當![]() 為偶數時,
為偶數時,![]()
當![]() 為奇數時,
為奇數時,![]()
所以,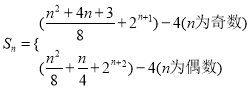 .
.
方法二:由題意知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…
,…
其中![]() ,
,![]() ,
,![]() ,
,![]() ,…
,…
![]() ,
,![]() ,
,![]() ,
,![]() …
…
觀察規律可知:下標為奇數的點的縱坐標為首項為![]() ,公比為4的等比數列,相鄰橫坐標之差為首項為2,公差為1的等差數列,下標為偶數的點也有此規律,并由數學歸納法可以證明.
,公比為4的等比數列,相鄰橫坐標之差為首項為2,公差為1的等差數列,下標為偶數的點也有此規律,并由數學歸納法可以證明.
所以,當![]() 為偶數時,
為偶數時,![]()
當![]() 為奇數時,
為奇數時,![]() ,
,
當![]() 為偶數時,
為偶數時,![]()
當![]() 為奇數時,
為奇數時,![]()
所以,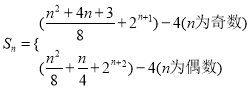 .
.


 南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案科目:高中數學 來源: 題型:
【題目】同學們有沒有讀過莎士比亞的名劇《威尼斯商人》?數學家斯摩林在劇中增加了一個情節:安東尼奧到鮑西婭家向她求婚,鮑西婭拿出一金、一銀、一鋁三個盒子,說:“每只盒子上寫了一句話,但只有一句是真的.誰能猜中我的肖象在哪只盒子中,才能做我的丈夫”.如果你是聰明、政治的安東尼奧,請問肖象在哪個盒子內?(請從金盒、銀盒、鋁盒中選擇一個填在橫線上)________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:如果一個數列從第2項起,每一項與它前一項的差都大于或等于2,則稱這個數列為“D數列”.
(1)若首項為1的等差數列![]() 的每一項均為正整數,且數列
的每一項均為正整數,且數列![]() 為“D數列”,其前n項和
為“D數列”,其前n項和![]() 滿足
滿足![]() (
(![]() ),求數列
),求數列![]() 的通項公式;
的通項公式;
(2)已知等比數列![]() 的每一項均為正整數,且數列
的每一項均為正整數,且數列![]() 為“D數列”,
為“D數列”,![]() ,設
,設 (
(![]() ),試判斷數列
),試判斷數列![]() 是否為“D數列”,并說明理由.
是否為“D數列”,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題14分)
如圖,在四棱錐P-ABCD中,底面ABCD為矩形,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,E,F分別為AD,PB的中點.
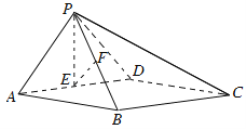
(Ⅰ)求證:PE⊥BC;
(Ⅱ)求證:平面PAB⊥平面PCD;
(Ⅲ)求證:EF∥平面PCD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三棱柱![]() 中,
中,![]() 為
為![]() 的中點,點
的中點,點![]() 在側棱
在側棱![]() 上,
上,![]() 平面
平面![]()
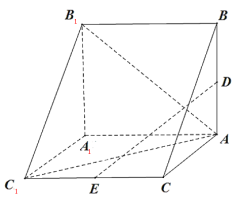
(1) 證明:![]() 是
是![]() 的中點;
的中點;
(2) 設![]() ,四邊形
,四邊形![]() 為邊長為4正方形,四邊形
為邊長為4正方形,四邊形![]() 為矩形,且異面直線
為矩形,且異面直線![]() 與
與![]() 所成的角為
所成的角為![]() ,求該三棱柱
,求該三棱柱![]() 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com