
【題目】定義:如果一個數(shù)列從第2項起,每一項與它前一項的差都大于或等于2,則稱這個數(shù)列為“D數(shù)列”.
(1)若首項為1的等差數(shù)列![]() 的每一項均為正整數(shù),且數(shù)列
的每一項均為正整數(shù),且數(shù)列![]() 為“D數(shù)列”,其前n項和
為“D數(shù)列”,其前n項和![]() 滿足
滿足![]() (
(![]() ),求數(shù)列
),求數(shù)列![]() 的通項公式;
的通項公式;
(2)已知等比數(shù)列![]() 的每一項均為正整數(shù),且數(shù)列
的每一項均為正整數(shù),且數(shù)列![]() 為“D數(shù)列”,
為“D數(shù)列”,![]() ,設(shè)
,設(shè) (
(![]() ),試判斷數(shù)列
),試判斷數(shù)列![]() 是否為“D數(shù)列”,并說明理由.
是否為“D數(shù)列”,并說明理由.
【答案】(1)![]() (2)是,理由見解析
(2)是,理由見解析
【解析】
(1) 設(shè)![]() 的公差為d,則
的公差為d,則![]() ,由
,由![]() 每一項均為正整數(shù),即
每一項均為正整數(shù),即![]() ,可求出
,可求出![]() .
.
(2).根據(jù)條件有![]() ,
,![]() ,,所以
,,所以![]() ,在數(shù)列
,在數(shù)列![]() 中,
中,![]() 為最小項,由數(shù)列
為最小項,由數(shù)列![]() 為“D數(shù)列”可知,只需
為“D數(shù)列”可知,只需![]() ,可求出
,可求出![]() ,
,![]() 或
或![]() ,
,![]() ,然后再分別
,然后再分別
判斷![]() 是否恒成立.
是否恒成立.
(1)設(shè)等差數(shù)列![]() 的公差為d,則
的公差為d,則![]() ,由
,由![]() ,得
,得![]() .
.
由題意得,![]() 對
對![]() 均成立,
均成立,
當(dāng)![]() 時,上式成立.當(dāng)
時,上式成立.當(dāng)![]() 時,
時,![]() ,
,
又![]() ,∴
,∴![]() ,∴
,∴![]()
∴等差數(shù)列![]() 的通項公式為
的通項公式為![]() .
.
(2)設(shè)等比數(shù)列![]() 的公比為q,則
的公比為q,則![]() ,
,
∵數(shù)列![]() 的每一項均為正整數(shù),且
的每一項均為正整數(shù),且![]() ,
,
∴![]() ,且q為整數(shù)
,且q為整數(shù)
∵![]() .
.
∴在數(shù)列![]() 中,
中,![]() 為最小項,由數(shù)列
為最小項,由數(shù)列![]() 為“D數(shù)列”可知,只需
為“D數(shù)列”可知,只需![]() .
.
即![]() ,又
,又![]() ,即
,即![]() .
.
由數(shù)列![]() 的每一項均為正整數(shù),可得
的每一項均為正整數(shù),可得![]() ,∴
,∴![]() ,
,![]() 或
或![]() ,
,![]() .①
.①
當(dāng)![]() ,
,![]() 時,
時,![]() ,則
,則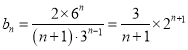 .
.
令![]() (
(![]() ),
), ![]()
則![]()
![]()
∴![]() .
. 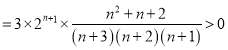
∴數(shù)列![]() 為遞增數(shù)列,即
為遞增數(shù)列,即![]() .又
.又![]() .
.
∴對任意的![]() 都有
都有![]() .
.
∴數(shù)列![]() 是“D數(shù)列”. ②
是“D數(shù)列”. ②
當(dāng)![]() ,
,![]() 時,
時,![]() ,則
,則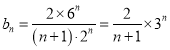 .
.
令![]() (
(![]() ).
).
![]()
![]() =
=![]()
∴![]()

∴數(shù)列![]() 為遞增數(shù)列,即
為遞增數(shù)列,即![]() .又
.又![]() .
.
∴對任意的![]() 都有
都有![]() ,∴數(shù)列
,∴數(shù)列![]() 是“D數(shù)列”.綜上,數(shù)列
是“D數(shù)列”.綜上,數(shù)列![]() 是“D數(shù)列”
是“D數(shù)列”


 暑假作業(yè)海燕出版社系列答案
暑假作業(yè)海燕出版社系列答案 本土教輔贏在暑假高效假期總復(fù)習(xí)云南科技出版社系列答案
本土教輔贏在暑假高效假期總復(fù)習(xí)云南科技出版社系列答案 暑假作業(yè)北京藝術(shù)與科學(xué)電子出版社系列答案
暑假作業(yè)北京藝術(shù)與科學(xué)電子出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知三棱錐![]() 的棱長均為6,其內(nèi)有
的棱長均為6,其內(nèi)有![]() 個小球,球
個小球,球![]() 與三棱錐
與三棱錐![]() 的四個面都相切,球
的四個面都相切,球![]() 與三棱錐
與三棱錐![]() 的三個面和球
的三個面和球![]() 都相切,如此類推,…,球
都相切,如此類推,…,球![]() 與三棱錐
與三棱錐![]() 的三個面和球
的三個面和球![]() 都相切(
都相切(![]() ,且
,且![]() ),則球
),則球![]() 的體積等于__________,球
的體積等于__________,球![]() 的表面積等于__________.
的表面積等于__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 滿足
滿足![]()
(1)當(dāng)![]() 時,寫出
時,寫出![]() 所有可能的值;
所有可能的值;
(2)當(dāng)![]() 時,若
時,若![]() 且
且![]() 對任意
對任意![]() 恒成立,求數(shù)列
恒成立,求數(shù)列![]() 的通項公式;
的通項公式;
(3)記數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,若
,若![]() 分別構(gòu)成等差數(shù)列,求
分別構(gòu)成等差數(shù)列,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() )的兩焦點與短軸兩端點圍成面積為12的正方形.
)的兩焦點與短軸兩端點圍成面積為12的正方形.
(1)求橢圓C的標(biāo)準(zhǔn)方程;
(2)我們稱圓心在橢圓上運動,半徑為![]() 的圓是橢圓的“衛(wèi)星圓”.過原點O作橢圓C的“衛(wèi)星圓”的兩條切線,分別交橢圓C于A、B兩點,若直線
的圓是橢圓的“衛(wèi)星圓”.過原點O作橢圓C的“衛(wèi)星圓”的兩條切線,分別交橢圓C于A、B兩點,若直線![]() 、
、![]() 的斜率為
的斜率為![]() 、
、![]() ,當(dāng)
,當(dāng)![]() 時,求此時“衛(wèi)星圓”的個數(shù).
時,求此時“衛(wèi)星圓”的個數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
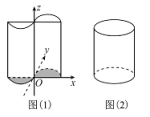
【題目】我國古代數(shù)學(xué)家祖暅提出原理:“冪勢既同,則積不容異”.其中“冪”是截面積,“勢”是幾何體的高.原理的意思是:夾在兩個平行平面間的兩個幾何體,被任一平行于這兩個平行平面的平面所截,若所截的兩個截面的面積恒相等,則這兩個幾何體的體積相等.如圖(1),函數(shù)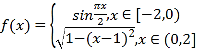 的圖象與x軸圍成一個封閉區(qū)域A(陰影部分),將區(qū)域A(陰影部分)沿z軸的正方向上移6個單位,得到一幾何體.現(xiàn)有一個與之等高的底面為橢圓的柱體如圖(2)所示,其底面積與區(qū)域A(陰影部分)的面積相等,則此柱體的體積為______.
的圖象與x軸圍成一個封閉區(qū)域A(陰影部分),將區(qū)域A(陰影部分)沿z軸的正方向上移6個單位,得到一幾何體.現(xiàn)有一個與之等高的底面為橢圓的柱體如圖(2)所示,其底面積與區(qū)域A(陰影部分)的面積相等,則此柱體的體積為______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某汽車美容公司為吸引顧客,推出優(yōu)惠活動:對首次消費的顧客,按![]() /次收費,并注冊成為會員,對會員逐次消費給予相應(yīng)優(yōu)惠,標(biāo)準(zhǔn)如下:
/次收費,并注冊成為會員,對會員逐次消費給予相應(yīng)優(yōu)惠,標(biāo)準(zhǔn)如下:
消費次第 | 第 | 第 | 第 | 第 |
|
收費比率 |
|
|
|
|
|
該公司注冊的會員中沒有消費超過![]() 次的,從注冊的會員中,隨機(jī)抽取了100位進(jìn)行統(tǒng)計,得到統(tǒng)計數(shù)據(jù)如下:
次的,從注冊的會員中,隨機(jī)抽取了100位進(jìn)行統(tǒng)計,得到統(tǒng)計數(shù)據(jù)如下:
消費次數(shù) |
|
|
|
|
|
人數(shù) |
|
|
|
|
|
假設(shè)汽車美容一次,公司成本為![]() 元,根據(jù)所給數(shù)據(jù),解答下列問題:
元,根據(jù)所給數(shù)據(jù),解答下列問題:
(1)某會員僅消費兩次,求這兩次消費中,公司獲得的平均利潤;
(2)以事件發(fā)生的頻率作為相應(yīng)事件發(fā)生的概率,設(shè)該公司為一位會員服務(wù)的平均利潤為![]() 元,求
元,求![]() 的分布列和數(shù)學(xué)期望
的分布列和數(shù)學(xué)期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一青蛙從點![]() 開始依次水平向右和豎直向上跳動,其落點坐標(biāo)依次是
開始依次水平向右和豎直向上跳動,其落點坐標(biāo)依次是![]()
![]() ,(如圖所示,
,(如圖所示,![]() 坐標(biāo)以已知條件為準(zhǔn)),
坐標(biāo)以已知條件為準(zhǔn)),![]() 表示青蛙從點
表示青蛙從點![]() 到點
到點![]() 所經(jīng)過的路程.
所經(jīng)過的路程.

(1)若點![]() 為拋物線
為拋物線![]() (
(![]() )準(zhǔn)線上一點,點
)準(zhǔn)線上一點,點![]() 均在該拋物線上,并且直線
均在該拋物線上,并且直線![]() 經(jīng)過該拋物線的焦點,證明
經(jīng)過該拋物線的焦點,證明![]() .
.
(2)若點![]() 要么落在
要么落在![]() 所表示的曲線上,要么落在
所表示的曲線上,要么落在![]() 所表示的曲線上,并且
所表示的曲線上,并且![]() ,試寫出
,試寫出![]() (不需證明);
(不需證明);
(3)若點![]() 要么落在
要么落在![]() 所表示的曲線上,要么落在
所表示的曲線上,要么落在![]() 所表示的曲線上,并且
所表示的曲線上,并且![]() ,求
,求![]() 的表達(dá)式.
的表達(dá)式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“雙11”促銷活動中,某商場為了吸引顧客,搞好促銷活動,采用“雙色球”定折扣的方式促銷,即:在紅、黃的兩個紙箱中分別裝有大小完全相同的紅、黃球各5個,每種顏色的5個球上標(biāo)有1,2,3,4,5等5個數(shù)字,顧客結(jié)賬時,先分別從紅、黃的兩個紙箱中各取一球,按兩個球的數(shù)字之和為折扣打折,如![]() ,就按3折付款,并規(guī)定取球后不再增加商品.按此規(guī)定,顧客享有6折及以下折扣的概率是( )
,就按3折付款,并規(guī)定取球后不再增加商品.按此規(guī)定,顧客享有6折及以下折扣的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 與函數(shù)
與函數(shù)![]() 的圖象有兩個不同的公共點
的圖象有兩個不同的公共點![]() 、
、![]() .
.
(1)求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)設(shè)點![]() 是線段
是線段![]() 的中點,證明:
的中點,證明:![]() .
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com