考點:三角函數的和差化積公式,三角函數的積化和差公式
專題:證明題,三角函數的求值
分析:(1)積化和差公式是由正弦或余弦的和角公式與差角公式通過加減運算推導而得.
(2)有了(1)積化和差的公式以后,我們只需一個變形,就可以得到和差化積的公式.我們把上述公式中的α+β設為θ,α-β設為φ,那么α=
(θ+φ),β=
(θ-φ),把α,β分別用θ,φ表示就可以得到和差化積的四個公式.
解答:
解:(1)①∵sin(α+β)=sinαcosβ+cosαsinβ,sin(α-β)=sinαcosβ-cosαsinβ,
∴把兩式相減,得到:cosαsinβ=
[sin(α+β)-sin(α-β)],
②∵cos(α+β)=cosαcosβ-sinαsinβ,cos(α-β)=cosαcosβ+sinαsinβ,
∴把兩式相加,得到:cos(α+β)+cos(α-β)=2cosαcosβ,
∴所以,cosαcosβ=
[cos(α+β)+cos(α-β)],
③∴同理,兩式相減,得到sinαsinβ=-
[cos(α+β)-cos(α-β)];
(2)把上述公式中的α+β設為θ,α-β設為φ,那么α=
,β=
,把α,β分別用θ,φ表示就可以得到和差化積的公式:
①∵由(1)得cosαsinβ=
[sin(α+β)-sin(α-β)],
∴cos
sin
=
[sinθ-sinφ],
∴sinθ-sinφ=2cos
sin
,
②∵由(1)得cosαcosβ=
[cos(α+β)+cos(α-β)],
∴cos
cos
=
[cosθ+cosφ],
∴cosθ+cosφ=2cos
cos
,
③∵由(1)得sinαsinβ=-
[cos(α+β)-cos(α-β)],
∴sin
sin
=-
[cosθ-cosφ],
∴cosθ-cosφ=-2sin
sin
.
點評:本題主要考查了三角函數的和差化積公式,三角函數的積化和差公式的證明,考查了轉化思想,屬于基本知識的考查.



 閱讀快車系列答案
閱讀快車系列答案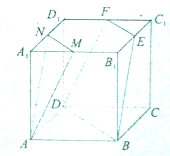 棱長為a的正方體ABCD-A1B1C1D1中,M、N、E、F分別為棱A1B1、A1D1、C1D1、B1C1的中點.
棱長為a的正方體ABCD-A1B1C1D1中,M、N、E、F分別為棱A1B1、A1D1、C1D1、B1C1的中點. 如圖,已知F是菱形ABCD的對角線的交點,平面ABCD⊥平面DEC,ED=
如圖,已知F是菱形ABCD的對角線的交點,平面ABCD⊥平面DEC,ED=