
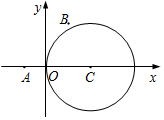
 如圖,在平面直角坐標(biāo)系xOy中,已知圓C:x2+y2-4x=0及點(diǎn)A(-1,0),B(1,2)
如圖,在平面直角坐標(biāo)系xOy中,已知圓C:x2+y2-4x=0及點(diǎn)A(-1,0),B(1,2)分析 (1)求出圓心C到直線l的距離,利用勾股定理建立方程,即可求直線l的方程;
(2)求出P的軌跡方程,利用兩圓的位置關(guān)系,即可得出結(jié)論.
解答 解:(1)圓C的標(biāo)準(zhǔn)方程為(x-2)2+y2=4,所以圓心C(2,0),半徑為2.
因?yàn)閘∥AB,A(-1,0),B(1,2),所以直線l的斜率為$\frac{2-0}{1-(-1)}=1$,
設(shè)直線l的方程為x-y+m=0,…(2分)
則圓心C到直線l的距離為$d=\frac{{|{2-0+m}|}}{{\sqrt{2}}}=\frac{{|{2+m}|}}{{\sqrt{2}}}$.…(4分)
因?yàn)?MN=AB=\sqrt{{2^2}+{2^2}}=2\sqrt{2}$,
而$C{M^2}={d^2}+{(\frac{MN}{2})^2}$,所以$4=\frac{{{{(2+m)}^2}}}{2}+2$,…(6分)
解得m=0或m=-4,
故直線l的方程為x-y=0或x-y-4=0.…(8分)
(2)假設(shè)圓C上存在點(diǎn)P,設(shè)P(x,y),則(x-2)2+y2=4,
PA2+PB2=(x+1)2+(y-0)2+(x-1)2+(y-2)2=12,
即x2+y2-2y-3=0,即x2+(y-1)2=4,…(10分)
因?yàn)?|2-2|<\sqrt{{{(2-0)}^2}+{{(0-1)}^2}}<2+2$,…(12分)
所以圓(x-2)2+y2=4與圓x2+(y-1)2=4相交,
所以點(diǎn)P的個(gè)數(shù)為2.…(14分)
點(diǎn)評(píng) 本題考查了直線與圓的方程的求法,考查了圓與圓的位置關(guān)系,是中檔題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
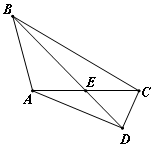 如圖,在四邊形ABCD中,|${\overrightarrow{AC}}$|=4,$\overrightarrow{BA}$•$\overrightarrow{BC}$=12,E為AC的中點(diǎn).
如圖,在四邊形ABCD中,|${\overrightarrow{AC}}$|=4,$\overrightarrow{BA}$•$\overrightarrow{BC}$=12,E為AC的中點(diǎn).查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 4,-1 | B. | -1 | C. | 1,-4 | D. | 4 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com