
【題目】已知函數f(x)=ex﹣axlnx.
(1)當a=1時,求曲線f(x)在x=1處的切線方程;
(2)證明:對于a∈(0,e),函數f(x)在區間(![]() )上單調遞增.
)上單調遞增.
【答案】(1)![]() ; (2)見解析.
; (2)見解析.
【解析】
(1)利用導數的幾何意義:切線斜率k=f′(1),切點(1,f(1)),由點斜式可得切線方程;
(2)求導,通過研究導函數的符號證明函數的單調性即可.
(1)當a=1時,f(x)=ex﹣xlnx(x>0)
∴f′(x)=ex﹣lnx﹣1,
∴f′(1)=e﹣1,
又∵f(1)=e,
∴曲線f(x)在x=1處的切線方程為y﹣e=(e﹣1),即y=(e﹣1)x+1
(2)∵f(x)=ex﹣axlnx,a∈(0,e),x∈(![]() ,1),
,1),
∴f′(x)=ex﹣a(1+lnx),
①當1+lnx≤0時,f′(x)>0恒成立,f(x)在(![]() ,1)上單調遞增;
,1)上單調遞增;
②當1+lnx>0即1≤a<e時,令g(x)=![]() ,
,
∴g′(x)=![]() =
=![]() ,
,
令h(x)=lnx﹣![]() +1,x∈(
+1,x∈(![]() ,1),
,1),
顯然h(x)在(![]() ,1)上單調遞增,且h(1)=0,
,1)上單調遞增,且h(1)=0,
∴h(x)<0在x∈(![]() ,1)上恒成立,∴g′(x)<0在x∈(
,1)上恒成立,∴g′(x)<0在x∈(![]() ,1)上恒成立,
,1)上恒成立,
故g(x)在(![]() ,1)上單調遞減,
,1)上單調遞減,
又g(1)=e,∴g(x)>g(1)=e在x∈(![]() ,1)上恒成立,
,1)上恒成立,
又1≤a<e,∴a<g(x)=![]() ,
,
∴ex﹣a(1+lnx)>0,
所以f(x)在區間(![]() ,1)上單調遞增.
,1)上單調遞增.
綜上可知,對a∈(0,e),函數f(x)在區間(![]() ,1)上單調遞增.
,1)上單調遞增.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】設一組數據的平均數是2.8,方差是3.6,若將這組數據中的每一個數據都加上10,得到一組新數據,則所得新數據的平均數和方差分別是( )
A.12.8 3.6 B.2.8 13.6 C.12.8 13.6 D.13.6 12.8
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 是圓柱的直徑,
是圓柱的直徑,![]() 是圓柱的母線,
是圓柱的母線,![]() ,
,![]() ,點
,點![]() 是圓柱底面圓周上的點.
是圓柱底面圓周上的點.
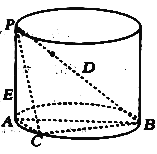
(1)求三棱錐![]() 體積的最大值;
體積的最大值;
(2)若![]() ,
,![]() 是線段
是線段![]() 上靠近點
上靠近點![]() 的三等分點,點
的三等分點,點![]() 是線段
是線段![]() 上的動點,求
上的動點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知直線![]() 和直線
和直線![]() ,射線
,射線![]() 的一個法向量為
的一個法向量為![]() ,點
,點![]() 為坐標原點,
為坐標原點,![]() ,
,![]() ,點
,點![]() 、
、![]() 分別是直線
分別是直線![]() 、
、![]() 上的動點,直線
上的動點,直線![]() 和
和![]() 之間的距離為2,
之間的距離為2,![]() 于點
于點![]() ,
,![]() 于點
于點![]() ;
;
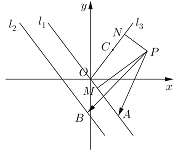
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的最大值;
的最大值;
(3)若![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)設![]() :實數x滿足|x﹣m|<2,設
:實數x滿足|x﹣m|<2,設![]() :實數x滿足
:實數x滿足![]() >1;若¬p是¬q的必要不充分條件,求實數m的取值范圍
>1;若¬p是¬q的必要不充分條件,求實數m的取值范圍
(2)已知p:函數f(x)=ln(x2﹣ax+3)的定義城為R,已知q:已知![]() 且
且![]() ,指數函數g(x)=(a﹣1)x在實數域內為減函數;若¬p∨q為假命題,求實數a的取值范圍.
,指數函數g(x)=(a﹣1)x在實數域內為減函數;若¬p∨q為假命題,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AB//CD,且![]()

(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱錐P-ABCD的體積為
,且四棱錐P-ABCD的體積為![]() ,求該四棱錐的側面積.
,求該四棱錐的側面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com