
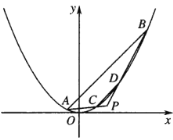
【題目】如圖,已知拋物線![]() ,直線
,直線![]() 交拋物線于
交拋物線于![]() ,
,![]() 兩點,
兩點,![]() 是拋物線外一點,連接
是拋物線外一點,連接![]() ,
,![]() 分別交拋物線于點
分別交拋物線于點![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)若![]() ,求點
,求點![]() 的軌跡方程;
的軌跡方程;
(Ⅱ)若![]() ,求
,求![]() 面積的最小值.
面積的最小值.
 挑戰100單元檢測試卷系列答案
挑戰100單元檢測試卷系列答案科目:高中數學 來源: 題型:
【題目】某學校為準備參加市運動會,對本校甲、乙兩個田徑隊中![]() 名跳高運動員進行了測試,并用莖葉圖表示出本次測試
名跳高運動員進行了測試,并用莖葉圖表示出本次測試![]() 人的跳高成績(單位:
人的跳高成績(單位:![]() ).跳高成績在
).跳高成績在![]() 以上(包括
以上(包括![]() )定義為“合格”,成績在
)定義為“合格”,成績在![]() 以下(不包括
以下(不包括![]() )定義為“不合格”.鑒于乙隊組隊晚,跳高成績相對較弱,為激勵乙隊隊隊,學校決定只有乙隊中“合格”者才能參加市運動會開幕式旗林隊.
)定義為“不合格”.鑒于乙隊組隊晚,跳高成績相對較弱,為激勵乙隊隊隊,學校決定只有乙隊中“合格”者才能參加市運動會開幕式旗林隊.
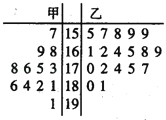
(1)求甲隊隊員跳高成績的中位數;
(2)如果用分層抽樣的方法從甲、乙兩隊所有的運動員中共抽取![]() 人,則
人,則![]() 人中“合格”與“不合格”的人數各為多少;
人中“合格”與“不合格”的人數各為多少;
(3)若從所有“合格”運動員中選取![]() 名,用
名,用![]() 表示所選運動員中能參加市運動會開幕式旗林隊的人數,試求
表示所選運動員中能參加市運動會開幕式旗林隊的人數,試求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=(sinx+cosx)2![]() cos(2x+π).
cos(2x+π).
(1)求函數f(x)的最小正周期;
(2)已知△ABC的內角A,B,C的對邊分別為a,b,c,若![]() ,且a=2,求△ABC的面積.
,且a=2,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】蜂巢是由工蜂分泌蜂蠟建成的.從正面看,蜂巢口是由許多正六邊形的中空柱狀體連接而成,中空柱狀體的底部是由三個全等的菱形面構成.如圖,在正六棱柱![]() 的三個頂點
的三個頂點![]() 處分別用平面
處分別用平面![]() ,平面
,平面![]() ,平面
,平面![]() 截掉三個相等的三棱錐
截掉三個相等的三棱錐![]() ,
,![]() ,
,![]() ,平面
,平面![]() ,平面
,平面![]() ,平面
,平面![]() 交于點
交于點![]() ,就形成了蜂巢的結構,如下圖(4)所示,
,就形成了蜂巢的結構,如下圖(4)所示,
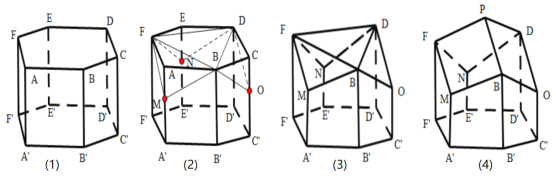
瑞士數學家克尼格利用微積分的方法證明了蜂巢的這種結構是在相同容積下所用材料最省的,英國數學家麥克勞林通過計算得到菱形的一個內角為![]() ,即
,即![]() .以下三個結論①
.以下三個結論①![]() ;②
;② ![]()
![]()
![]() ;③
;③![]() 四點共面,正確命題的個數為______個;若
四點共面,正確命題的個數為______個;若![]() ,
,![]() ,
,![]() ,則此蜂巢的表面積為_______.
,則此蜂巢的表面積為_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 的參數方程為
的參數方程為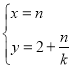 (
(![]() 為參數).設直線
為參數).設直線![]() 與
與![]() 的交點為
的交點為![]() ,當
,當![]() 變化時的點
變化時的點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求出曲線![]() 的普通方程;
的普通方程;
(2)以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,設射線
軸正半軸為極軸建立極坐標系,設射線![]() 的極坐標方程為
的極坐標方程為![]() 且
且![]() ,點
,點![]() 是射線
是射線![]() 與曲線
與曲線![]() 的交點,求點
的交點,求點![]() 的極徑.
的極徑.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋子中有四張卡片,分別寫有“國”、“富”、“民”、“強”四個字,有放回地從中任取一張卡片,將三次抽取后“國”“富”兩個字都取到記為事件A,用隨機模擬的方法估計事件A發生的概率,利用電腦隨機產生整數0,1,2,3四個隨機數,分別代表“國”、“富”、“民”、“強”這四個字,以每三個隨機數為一組,表示取卡片三次的結果,經隨機模擬產生了以下18組隨機數:
231 | 232 | 210 | 023 | 122 | 021 | 321 | 220 | 031 |
231 | 103 | 133 | 132 | 001 | 320 | 123 | 130 | 233 |
由此可以估計事件A發生的概率為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖的多面體中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中點.
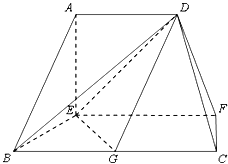
(Ⅰ)求證:AB∥平面DEG;
(Ⅱ)求證:BD⊥EG;
(Ⅲ)求多面體ADBEG的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com